Transformaciones Delta-Estrella

Ahora podemos resolver redes resistivas simples en serie, en paralelo o tipo puente usando las leyes de Circuito de Kirchhoff, técnicas de análisis de corriente de malla o análisis de voltaje nodal, pero en un circuito trifásico balanceado podemos usar diferentes técnicas matemáticas para simplificar el análisis del circuito y así reducir la cantidad de matemáticas involucradas, lo que en sí mismo es algo bueno.

Los circuitos o redes trifásicas estándar adoptan dos formas principales con nombres que representan la forma en que se conectan las resistencias, una red de estrella conectada que tiene el símbolo de la letra, Υ (estrella) y una red Delta conectada que tiene el símbolo de un triángulo, Δ (delta).

Si se conecta un suministro trifásico, trifásico o incluso una carga trifásica en un tipo de configuración, se puede transformar o cambiar fácilmente a una configuración equivalente del otro tipo utilizando la Transformación Star Delta o transformación Delta-Estrella.

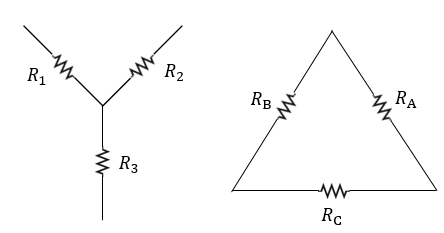
Se puede conectar una red resistiva que consta de tres impedancias para formar una configuración en T o en “T”, pero la red también se puede volver a dibujar para formar una Estrella o red tipo Υ como se muestra a continuación:

Red equivalente en estrella y conectada en T

Como ya hemos visto, podemos volver a dibujar la red de resistencia anterior T para producir una estrella  eléctricamente equivalente o red de tipo Y. Pero también podemos convertir una Pi o red de tipo resistencia π en una eléctricamente equivalente Delta o red de tipo Δ, como se muestra a continuación:

Red equivalente Delta y conectada a Pi

Habiendo definido ahora exactamente qué es una red conectada en estrella y en triángulo, es posible transformar el Υ en un circuito equivalente Δ y también convertir un Δ en un circuito equivalente Υ utilizando un proceso de transformación.

Este proceso nos permite producir una relación matemática entre las diversas resistencias, lo que nos da una Transformación Estrella-Delta y una Transformación Delta-Estrella.

Estas transformaciones de circuito nos permiten cambiar las tres resistencias conectadas (o impedancias) por sus equivalentes medidos entre los terminales 1-2, 1-3 o 2-3 para un circuito conectado en estrella o en triángulo. Sin embargo, las redes resultantes solo son equivalentes para voltajes y corrientes externas a las redes estrella o delta, ya que internamente los voltajes y corrientes son diferentes pero cada red consumirá la misma cantidad de energía y tendrá el mismo factor de potencia entre sí.

Transformación en delta-estrella

Para convertir una red delta en una red estrella equivalente, necesitamos derivar una fórmula de transformación para equiparar las distintas resistencias entre las distintas terminales. Considere el circuito a continuación:

Red Delta a Estrella

Compare las resistencias entre los terminales 1 y 2.

Resistencia entre los terminales 2 y 3.

Resistencia entre los terminales 1 y 3.

Esto ahora nos da tres ecuaciones y tomando la ecuación 3 de la ecuación 2 da:

Entonces, reescribiendo la Ecuación 1 nos dará:

Sumando la ecuación 1 y el resultado anterior de la ecuación 3 menos la ecuación 2 da:

De lo cual nos da la ecuación final para resistencia P como:

Luego, para resumir un poco sobre las matemáticas anteriores, ahora podemos decir que la resistencia P en una red en estrella se puede encontrar como Ecuación 1 más (Ecuación 3 menos Ecuación 2) o  Eq1 + (Eq3 – Eq2).

De manera similar, para encontrar el resistor Q en una red en estrella, es la ecuación 2 más el resultado de la ecuación 1 menos la ecuación 3 o  Eq2 + (Eq1 – Eq3) y esto nos da la transformación de Q como:

Y nuevamente, para encontrar el resistor R en un Red en estrella, es la ecuación 3 más el resultado de la ecuación 2 menos la ecuación 1 o  Eq3 + (Eq2 – Eq1) y esto nos da la transformación de R como:

Al convertir una red delta en una red en estrella los denominadores de todas las fórmulas de transformación son los mismos: A + B + C, y que es la suma de TODAS las resistencias delta. Luego, para convertir cualquier red conectada delta en una red en estrella equivalente, podemos resumir las ecuaciones de transformación anteriores como:

Ecuaciones de transformaciones delta a estrella

Si las tres resistencias en la red delta son todas iguales en valor, las resistencias resultantes en la red en estrella equivalente serán iguales a un tercio del valor de las resistencias delta. Esto le da a cada rama resistiva en la red en estrella un valor de: RSTAR1/3 =* RDELTA que es lo mismo que decir: (RDELTA) / 3

Ejemplo  Delta-Estrella No.1

Convierta la siguiente Red Delta Resistiva en una red equivalente Estrella.

Transformación Estrella-Delta

La transformación Estrella-Delta es simplemente lo contrario de lo anterior. Hemos visto que al convertir de una red delta a una red equivalente estrella, la resistencia conectada a un terminal es el producto de las dos resistencias delta conectadas al mismo terminal, por ejemplo, la resistencia P es el producto de las resistencias A y B conectadas a terminal 1.

Al reescribir un poco las fórmulas anteriores, también podemos encontrar las fórmulas de transformación para convertir una red en estrella resistiva en una red equivalente delta que nos da una forma de producir una transformación Estrella-Delta como se muestra a continuación: 

Transformación de estrella a delta

El valor de la resistencia en cualquier lado de la red delta, Δ, es la suma de todas las combinaciones de dos productos de resistencias en la red en estrella dividida por la resistencia en estrella ubicada «directamente opuesta» a la resistencia delta que se encuentra . Por ejemplo, el resistor A se da como:

con respecto al terminal 3 y el resistor B se da como:

con respecto al terminal 2 con el resistor C dado como:

con respecto al terminal 1.

Al dividir cada ecuación por el valor del denominador, terminará con tres fórmulas de transformación separadas que se pueden usar para convertir cualquier red resistiva Delta en una red en estrella equivalente como se indica a continuación:

Ecuaciones de transformación Estrella-Delta

Un último punto sobre la conversión de una red resistiva en estrella en una red equivalente delta. Si todas las resistencias en la red en estrella son todas iguales en valor, las resistencias resultantes en la red equivalente delta serán tres veces el valor de las resistencias en estrella y serán iguales, dando:  RDELTA = 3 * RSTAR

Ejemplo Estrella-Delta No.2

Convertir la siguiente red Estrella Resistiva en una red Delta equivalente.

Tanto la transformación Estrella-Delta como la transformación Delta-Estrella nos permiten convertir un tipo de conexión de circuito en otro tipo para que podamos analizar fácilmente el circuito. Estas técnicas de transformación se pueden utilizar con buenos resultados para circuitos en estrella o delta que contienen resistencias o impedancias.