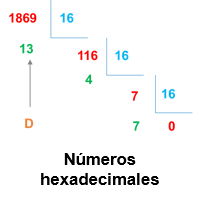
Los números hexadecimales agrupan números binarios en conjuntos de cuatro, lo que permite la conversión de 16 dígitos binarios diferentes.
La principal desventaja de los números binarios es que la cadena binaria equivalente a un gran número decimal de base 10 puede ser bastante larga.
Cuando se trabaja con grandes sistemas digitales, como computadoras, es común encontrar números binarios que constan de 8, 16 e incluso 32 dígitos, lo que dificulta tanto la lectura como la escritura sin producir errores, especialmente cuando se trabaja con lotes de 16 o 32 bits números binarios.
Una forma común de superar este problema es organizar los números binarios en grupos o conjuntos de cuatro bits (4 bits). Estos grupos de 4 bits utilizan otro tipo de sistema de numeración que también se usa comúnmente en sistemas informáticos y digitales llamados números hexadecimales.

Cadena numérica hexadecimal
El sistema de numeración «Hexadecimal» o simplemente «Hex» utiliza el sistema Base de 16 y es una opción popular para representar valores binarios largos porque su formato es bastante compacto y mucho más fácil de entender en comparación con las cadenas binarias largas de 1 y 0’s.
Al ser un sistema Base-16, el sistema de numeración hexadecimal utiliza 16 (dieciséis) dígitos diferentes con una combinación de números del 0 al 15. En otras palabras, hay 16 símbolos de dígitos posibles.
Sin embargo, existe un problema potencial con el uso de este método de notación de dígitos causado por el hecho de que los números decimales de 10, 11, 12, 13, 14 y 15 se escriben normalmente usando dos símbolos adyacentes. Por ejemplo, si escribimos 10 en hexadecimal, ¿nos referimos al número decimal diez o al número binario de dos (1 + 0)? Para sortear este complicado problema, los números hexadecimales que identifican los valores de diez, once,. . ., quince y se reemplazan con letras mayúsculas de A, B, C, D, E y F respectivamente.
Luego, en el sistema de numeración hexadecimal , usamos los números del 0 al 9 y las letras mayúsculas de la A a la F para representar su número binario o decimal equivalente, comenzando con el dígito menos significativo en el lado derecho.
Como acabamos de decir, las cadenas binarias pueden ser bastante largas y difíciles de leer, pero podemos hacer la vida más fácil dividiendo estos grandes números binarios en grupos pares para que sean mucho más fáciles de escribir y comprender. Por ejemplo, el siguiente grupo de dígitos binarios 1101 0101 1100 11112 es mucho más fácil de leer y comprender que 11010101110011112 cuando están todos agrupados.
En el uso diario del sistema de numeración decimal, usamos grupos de tres dígitos o 000 del lado derecho para hacer que un número muy grande, como un millón o un billón, sea más fácil de entender para nosotros y lo mismo ocurre con los sistemas digitales.
Números hexadecimales es un sistema más complejo que usar solo binario o decimal y se usa principalmente cuando se trata de computadoras y ubicaciones de direcciones de memoria. Al dividir un número binario en grupos de 4 bits, cada grupo o conjunto de 4 dígitos ahora puede tener un valor posible de entre «0000» (0) y «1111» (8 + 4 + 2 + 1 = 15) dando un total de 16 combinaciones de números diferentes del 0 al 15. No olvide que “0” también es un dígito válido.
Recordamos de nuestro primer tutorial sobre números binarios que un grupo de dígitos de 4 bits se llama «nibble» y como también se requieren 4 bits para producir un número hexadecimal, un dígito hexadecimal también se puede considerar como un nibble, o medio byte. Luego, se requieren dos números hexadecimales para producir un byte completo que va de 00 a FF.
Además, dado que 16 en el sistema decimal es la cuarta potencia de 2 (o 24 ), existe una relación directa entre los números 2 y 16, por lo que un dígito hexadecimal tiene un valor igual a cuatro dígitos binarios, por lo que ahora q es igual a » dieciséis».
Debido a esta relación, cuatro dígitos de un número binario se pueden representar con un solo dígito hexadecimal. Esto hace que la conversión entre números binarios y hexadecimales sea muy fácil, y el hexadecimal se puede utilizar para escribir números binarios grandes con muchos menos dígitos.
Los números del 0 al 9 todavía se usan como en el sistema decimal original, pero los números del 10 al 15 ahora están representados por letras mayúsculas del alfabeto de la A a la F inclusive y la relación entre decimal, binario y hexadecimal se da a continuación.
Contenido
Números hexadecimales
| Número decimal | Número binario de 4 bits | Número hexadecimal |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
| 16 | 0001 0000 | 10 (1 + 0) |
| 17 | 0001 0001 | 11 (1 + 1) |
| Continuando hacia arriba en grupos de cuatro |
Usando el número binario original de arriba 1101 0101 1100 11112 esto ahora se puede convertir en un número hexadecimal equivalente de ceros D5CF que es mucho más fácil de leer y comprender que una larga fila de unos y ceros que teníamos antes.
Entonces, al usar la notación hexadecimal, los números digitales se pueden escribir usando menos dígitos y con mucha menos probabilidad de que ocurra un error. De manera similar, convertir números basados en hexadecimales nuevamente en binarios es simplemente la operación inversa.
Entonces, las principales características de un sistema de numeración hexadecimal es que hay 16 dígitos de conteo distintos de 0 a F, y cada dígito tiene un peso o valor de 16 a partir del bit menos significativo (LSB). Para distinguir los números hexadecimales de los números denarios, se usa un prefijo de “#”, (Hash) o “$” (signo de dólar) antes del real número hexadecimal de valor, # D5CF o $ D5CF.
Como la base de un sistema hexadecimal es 16, que también representa el número de símbolos individuales usados en el sistema, el subíndice 16 se usa para identificar un número expresado en hexadecimal. Por ejemplo, el número hexadecimal anterior se expresa como: D5CF16
Contar usando números hexadecimales
Ahora sabemos cómo convertir 4 dígitos binarios en un número hexadecimal. Pero, ¿si tuviéramos más de 4 qué pasaría con dígitos binarios, cómo contaríamos en hexadecimal más allá de la letra final F? La respuesta simple es comenzar de nuevo con otro conjunto de 4 bits de la siguiente manera.
0… a… 9, A, B, C, D, E, F, 10… a… 19, 1A, 1B, 1C, 1D, 1E, 1F, 20, 21… .etc
No se confunda, 10 o 20 no es diez o veinte, es 1 + 0 y 2 + 0 en hexadecimal. De hecho, veinte ni siquiera existen en hexadecimal. Con dos números hexadecimales podemos contar hasta FF que es igual al decimal 255. Del mismo modo, para contar más alto que FF , agregaríamos un tercer dígito hexadecimal a la izquierda para que el primer número hexadecimal de 3 bits sea 10016, (25610) y el último sería FFF16, (409510). El número hexadecimal máximo de 4 dígitos es FFFF16 , que es igual a 65 535 en decimal y así sucesivamente.
Representación de un número hexadecimal
| MSB | Número hexadecimal | LSB | ||||||
| 168 | 167 | 166 | 165 | 164 | 163 | 162 | 161 | 160 |
| 4.3G | 2.6G | 16M | 1M | 65k | 4k | 256 | 16 | 1 |
Esta suma de dígitos hexadecimales adicionales para convertir tanto decimal como binario números en un número hexadecimal es muy fácil si hay 4, 8, 12 o 16 dígitos binarios para convertir. Pero también podemos agregar ceros a la izquierda del bit más significativo, el MSB, si el número de bits binarios no es múltiplo de cuatro.
Por ejemplo, 110010110110012 es un número binario de catorce bits que es demasiado grande para solo tres dígitos hexadecimales, pero demasiado pequeño para un número hexadecimal de cuatro. La respuesta es AGREGAR ceros adicionales al bit más a la izquierda hasta que tengamos un conjunto completo de números binarios de cuatro bits o múltiplos del mismo.
Sumar ceros adicionales a un número binario
| Número binario | 0011 | 0010 | 1101 | 1001 |
| Número hexadecimal | 3 | 2 | D | 9 |
La principal ventaja de un número hexadecimal es que es muy compacto y al usar una base de 16 significa que el número de dígitos usados para representar un número dado suele ser menor que en binario o decimal. Además, es rápido y fácil convertir entre números hexadecimales y binarios.
Ejemplo de números hexadecimales No.1
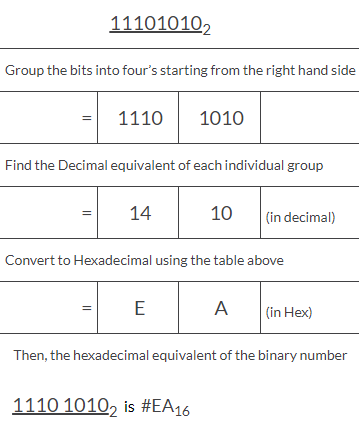
Convierta el siguiente número binario 1110 10102 en su número hexadecimal equivalente.
Ejemplo de números hexadecimales No.2
Convierta el siguiente número hexadecimal # 3FA716 en su equivalente binario, y también en su equivalente decimal o denario usando subíndices para identificar cada sistema de numeración.
| # 3FA716 |
| = 0011 1111 1010 01112 |
| = (8192 + 4096 + 2048 + 1024 + 512 + 256 + 128 + 32 + 4 + 2 + 1) |
| = 16,29510 |
Entonces, el número decimal de 16.295 se puede representar como:
# 3FA716 en hexadecimal
o
0011 1111 1010 01112 en binario.
Resumen de números hexadecimales
A continuación, para resumir el hexadecimal o sistema de numeración hexadecimal se usa comúnmente en sistemas informáticos y digitales para reducir grandes cadenas de números binarios en conjuntos de cuatro dígitos para que podamos entenderlos fácilmente. La palabra «hexadecimal» significa dieciséis porque este tipo de sistema de numeración digital utiliza 16 dígitos diferentes del 0 al 9 y de la A a la F.
Los números hexadecimales agrupan números binarios en conjuntos de cuatro dígitos. Para convertir una secuencia binaria en un equivalente número hexadecimal, primero debemos agrupar los dígitos binarios en un conjunto de 4 bits. Estos conjuntos binarios pueden tener cualquier valor de 010 (00002 ) a 1510 (11112 ) que representa el equivalente hexadecimal de 0 hasta F.En el próximo tutorial sobre lógica binaria , veremos cómo convertir cadenas enteras de números binarios en otro sistema de numeración digital llamado Octal Numbers y viceversa.