Se consideran inductores en serie cuando están conectados en cadena y comparten una corriente eléctrica común.
Estas interconexiones de inductores producen redes más complejas cuya inductancia general es una combinación de los inductores individuales. Sin embargo, existen ciertas reglas para conectar inductores en serie o en paralelo y se basan en el hecho de que no existe inductancia mutua o acoplamiento magnético entre los inductores individuales.
Se dice que los inductores están conectados en «serie» cuando están conectados en cadena en línea recta, de un extremo a otro. En el tutorial de Resistores en serie vimos que los diferentes valores de las resistencias conectadas entre sí en serie simplemente se “suman” y esto también es cierto para la inductancia. Los inductores en serie simplemente se “suman” porque el número de vueltas de la bobina aumenta efectivamente, siendo la inductancia total del circuito LT igual a la suma de todas las inductancias individuales sumadas.
Contenido
Inductor de circuito en serie

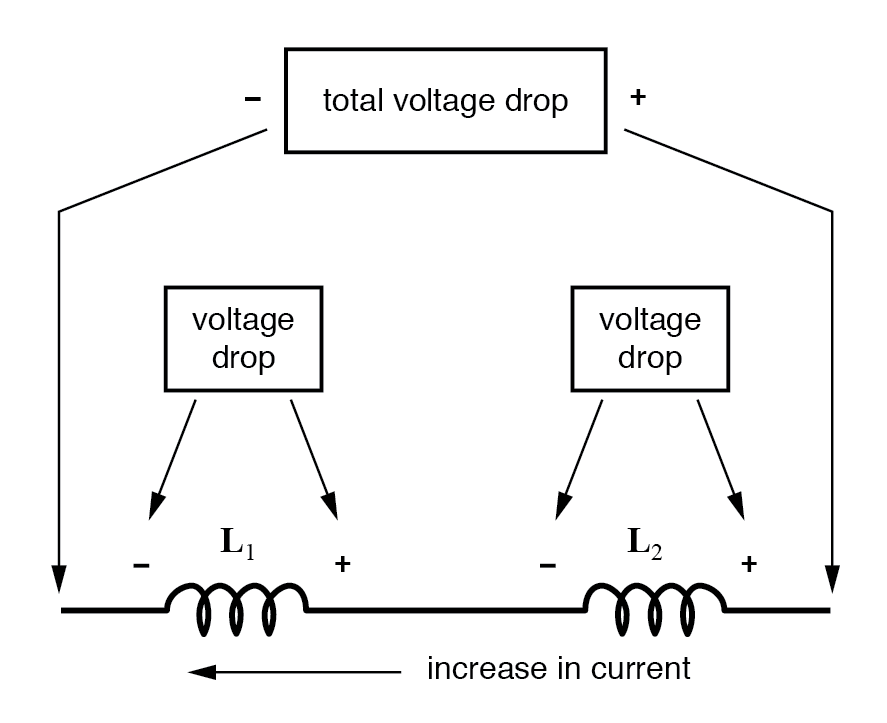
La corriente, ( I ) que fluye a través del primer inductor, L1 no tiene otro camino por recorrer que pasar por el segundo inductor y el tercero y así sucesivamente. Luego, los inductores en serie tienen una corriente común que fluye a través de ellos, por ejemplo:
IL1 = IL2 = IL3 = IAB … etc.
En el ejemplo anterior, los inductores L1, L2 y L3 están todos conectados entre sí en serie entre los puntos A y B. La suma de las caídas de voltaje individuales en cada inductor se puede encontrar usando la Ley de voltaje de Kirchoff (KVL) donde, VT = V1 + V2 + V3 y sabemos por los tutoriales anteriores sobre inductancia que la fem autoinducida a través de un inductor se da como: V = L di / dt.
Entonces, al tomar los valores de las caídas de voltaje individuales en cada inductor en nuestro ejemplo anterior, la inductancia total para la combinación en serie se da como:

Al dividir la ecuación anterior por di / dt , podemos reducirla para dar una expresión final para calcular la inductancia total de un circuito cuando se conectan inductores en serie y esto se da como:
Ecuación de inductores en serie
Ltotal = L1 + L2 + L3 +… + Ln etc.
Entonces, la inductancia total de la cadena en serie se puede encontrar simplemente sumando las inductancias individuales de los inductores en serie, al igual que sumar resistencias en serie. Sin embargo, la ecuación anterior sólo es válida cuando hay inductancia mutua «NO» o acoplamiento magnético entre dos o más de los inductores (están magnéticamente aislados entre sí).
Un punto importante para recordar acerca de los inductores en circuitos en serie, la inductancia total ( LT ) de dos o más inductores conectados en serie siempre será MAYOR que el valor del inductor más grande en la cadena en serie.
Ejemplo de Inductores en serie No.1
Tres inductores de 10 mH, 40 mH y 50 mH están conectados juntos en una combinación en serie sin inductancia mutua entre ellos. Calcule la inductancia total de la combinación en serie.

Inductores conectados mutuamente en serie
Cuando los inductores están conectados en serie de modo que el campo magnético de uno se vincula con el otro, el efecto de la inductancia mutua aumenta o disminuye la inductancia total dependiendo de la cantidad de acoplamiento magnético. El efecto de esta inductancia mutua depende de la distancia entre las bobinas y su orientación entre sí.
Los inductores en serie conectados mutuamente pueden clasificarse como «auxiliares» u «opuestos» a la inductancia total. Si el flujo magnético producido por la corriente fluye a través de las bobinas en la misma dirección, se dice que las bobinas están acopladas acumulativamente. Si la corriente fluye a través de las bobinas en direcciones opuestas, se dice que las bobinas están acopladas diferencialmente como se muestra a continuación.
Inductores en serie acoplados acumulativamente

Si bien la corriente que fluye entre los puntos A y D a través de las dos bobinas acopladas acumulativamente está en la misma dirección, la ecuación anterior para las caídas de voltaje en cada una de las bobinas debe modificarse para tener en cuenta la interacción entre las dos bobinas debido a la efecto de la inductancia mutua. La autoinductancia de cada bobina individual, L1 y L2 respectivamente, será la misma que antes, pero con la adición de M que denota la inductancia mutua.
Entonces, la fem total inducida en las bobinas acopladas acumulativamente se da como:

Donde: 2M representa la influencia de la bobina L1 sobre L2 e igualmente la bobina L2 sobre L1.
Al dividir la ecuación anterior por di / dt , podemos reducirla para obtener una expresión final para calcular la inductancia total de un circuito cuando los inductores están conectados acumulativamente y esto se da como:
Ltotal = L 1 + L 2 + 2M
Si una de las bobinas se invierte para que la misma corriente fluya a través de cada bobina pero en direcciones opuestas, la inductancia mutua, M que existe entre las dos bobinas tendrá un efecto de cancelación en cada bobina como se muestra a continuación.
Inductores en serie acoplados diferencialmente

La fem que se induce en la bobina 1 por el efecto de la inductancia mutua de la bobina dos está en oposición a la fem autoinducida en la bobina uno, ya que ahora la misma corriente pasa a través de cada bobina en direcciones opuestas. Para tener en cuenta este efecto de cancelación, se usa un signo menos con M cuando el campo magnético de las dos bobinas está conectado diferencialmente, lo que nos da la ecuación final para calcular la inductancia total de un circuito cuando los inductores están conectados diferencialmente como:
Ltotal = L 1 + L 2 – 2M
Entonces, la ecuación final para inductores acoplados inductivamente en serie se da como:

Ejemplo de Inductores en serie No.2
Dos inductores de 10mH respectivamente están conectados juntos en una combinación en serie para que sus campos magnéticos se ayuden entre sí dando un acoplamiento acumulativo. Su inductancia mutua se expresa como 5 mH. Calcule la inductancia total de la combinación en serie.

Ejemplo de Inductores en serie No.3
Dos bobinas conectadas en serie tienen una autoinducción de 20 mH y 60 mH respectivamente. Se encontró que la inductancia total de la combinación era 100 mH. Determine la cantidad de inductancia mutua que existe entre las dos bobinas asumiendo que se ayudan entre sí.

Resumen de Inductores en serie
Ahora sabemos que podemos conectar inductores en serie para producir un valor de inductancia total, LT igual a la suma de los valores individuales, se suman, similar a conectar resistencias en serie. Sin embargo, cuando se conectan inductores en serie, pueden verse afectados por la inductancia mutua.
Los inductores en serie conectados mutuamente se clasifican como «auxiliares» u «opuestos» a la inductancia total dependiendo de si las bobinas están acopladas acumulativamente (en la misma dirección) o acopladas diferencialmente (en dirección opuesta).En el próximo tutorial sobre Inductores, veremos que la posición de las bobinas cuando se conectan Inductores en Paralelo también afecta la inductancia total, LT del circuito.