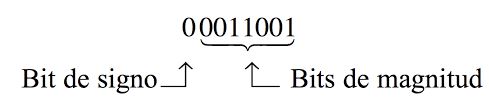Números binarios con signo

En matemáticas, los números positivos (incluido el cero) se representan como números sin signo. Es decir, no ponemos el signo + delante de ellos para mostrar que son números positivos.

Sin embargo, cuando se trata de números negativos, usamos un signo – delante del número para mostrar que el número tiene un valor negativo y es diferente de un valor positivo sin signo, y lo mismo ocurre con los números binarios con signo.

Sin embargo, en los circuitos digitales no existe ninguna disposición para poner un signo más o incluso un signo menos a un número, ya que los sistemas digitales operan con números binarios que se representan en términos de «0» y «1». Cuando se usan juntos en microelectrónica, estos «1» y «0», llamados un bit (que es una contracción de BInary digiT), caen en varios tamaños de rango de números a los que se hace referencia por nombres comunes, como un byte o una palabra.

También hemos visto anteriormente que un número binario de 8 bits (un byte) puede tener un valor que va desde 0 (00000000₂) a 255 (11111111₂), es decir, 2⁸ = 256 combinaciones diferentes de bits que forman un sólo 8 bits byte. Entonces, por ejemplo, un número binario sin signo como: 01001101₂= 64 + 8 + 4 + 1 = 77₁₀ en decimal. Pero los sistemas digitales y las computadoras también deben poder usar y manipular números negativos y números positivos.

Los números matemáticos generalmente se componen de un signo y un valor (magnitud) en el que el signo indica si el número es positivo, ( + ) o negativo, ( – ) con el valor que indica el tamaño del número, por ejemplo 23, + 156 o -274. La presentación de números de esta manera se denomina representación de «signo-magnitud», ya que el dígito más a la izquierda se puede usar para indicar el signo y los dígitos restantes la magnitud o el valor del número.

La notación de magnitud de signo es el método más simple y uno de los más comunes para representar números positivos y negativos a ambos lados del cero, (0). Por lo tanto los números negativos se obtienen simplemente cambiando el signo del número positivo correspondiente, ya que cada número positivo o sin firma tendrá un opuesto firmado, por ejemplo, 2 y -2, 10 y -10, etc .

Pero ¿cómo lo representamos firmaron números binarios si todo lo que tenemos es un montón de unos y ceros. Sabemos que los dígitos binarios, o bits, solo tienen dos valores, ya sea un “1” o un “0” y, convenientemente para nosotros, un signo también tiene solo dos valores, siendo un “+” o un “–”.

Luego, podemos usar un solo bit para identificar el signo de un número binario con signo como de valor positivo o negativo. Entonces, para representar un número binario positivo (+ n) y un número negativo (-nbinario), podemos usarlos con la adición de un signo.

Para números binarios con signo, el bit más significativo (MSB) se utiliza como bit de signo. Si el bit de signo es «0», esto significa que el número tiene un valor positivo. Si el bit de signo es «1», entonces el número tiene un valor negativo. Los bits restantes del número se utilizan para representar la magnitud del número binario en la forma habitual de formato de número binario sin signo.

Luego podemos ver que la notación de signo y magnitud (SM) almacena valores positivos y negativos al dividir los “n” bits totales en dos partes: 1 bit para el signo y n – 1 bits para el valor que es un número binario puro. Por ejemplo, el número decimal 53 se puede expresar como un número binario con signo de 8 bits de la siguiente manera.

Números positivos binarios con signo 

Números negativos binarios con signo

La desventaja aquí es que mientras que antes teníamos un rango completo de n bits binarios con número binario sin signo, ahora tenemos un número binario con signo de n-1 bit que da un rango reducido de dígitos de:

-2^(n-1)  a  +2^(n-1)

Entonces, por ejemplo: si tenemos 4 bits para representar un número binario con signo, (1 bit para el bit de signo y 3 bits para los bits de magnitud), entonces el rango real de los números que podemos representar en notación de magnitud de signo serían:

-2^(4-1) – 1    a +2^(4-1) – 1

-2⁽³⁾ – 1    a    +2⁽³⁾ – 1

-7    a    +7

Mientras que antes, el rango de un número binario de 4 bits sin signo habría sido de 0 a 15, o de 0 a F en hexadecimal, ahora tenemos un rango reducido de -7 a +7. Por lo tanto, un número binario sin signo no tiene un solo bit de signo y, por lo tanto, puede tener un rango binario más grande, ya que el bit más significativo (MSB) es solo un bit o dígito adicional en lugar de un bit de signo usado.

Otra desventaja aquí de la forma signo-magnitud es que podemos tener un resultado positivo para cero, +0 o 0000₂, y un resultado negativo para cero, -0 o 1000₂. Ambos son válidos pero cuál es el correcto.

Ejemplos de los números binarios con signo No.1

Convertir los siguientes valores decimales en números binarios con signo usando el formato de señal de magnitud:

-1510    como un número de 6 bits	⇒	1011112
+2310  como un número de 6 bits	⇒	0101112
-5610  como un número de 8 bits	⇒	101110002
+8510  como un número de 8 bits	⇒	010101012
-12710  como un número de 8 bits	⇒	111111112

Nota que para un 4 bits, 6 bits, 8- bit, número binario de 16 bits o 32 bits con signo, todos los bits DEBEN tener un valor, por lo tanto, se utilizan «ceros» para llenar los espacios entre el bit de signo más a la izquierda y el primer valor o el valor más alto «1».

La representación en signo de magnitud de un número binario es un método simple de usar y comprender para representar números binarios con signo, ya que usamos este sistema todo el tiempo con números decimales normales (base 10) en matemáticas. Agregar un «1» al frente si el número binario es negativo y un «0» si es positivo.

Sin embargo, el uso de este método de magnitud de signo puede dar como resultado la posibilidad de que dos patrones de bits diferentes tengan el mismo valor binario. Por ejemplo, +0 y -0 serían 0000 y 1000 respectivamente como un número binario de 4 bits con signo. Entonces podemos ver que usando este método puede haber dos representaciones para cero, un cero positivo ( 0000₂ ) y también un cero negativo ( 1000₂ ) lo que puede causar grandes complicaciones para computadoras y sistemas digitales.

El complemento de uno en un número binario con signo

El complemento de uno, es otro método que podemos usar para representar números binarios negativos en un sistema numérico binario con signo. En el complemento de uno, los números positivos (también conocidos como no complementos) permanecen sin cambios como antes con los números de magnitud de signo.

Sin embargo, los números negativos se representan tomando el complemento a uno (inversión, negación) del número positivo sin signo. Dado que los números positivos siempre comienzan con un «0», el complemento siempre comenzará con un «1» para indicar un número negativo.

El complemento a uno de un número binario negativo es el complemento de su contraparte positivo, por lo que para tomar el complemento a uno de un número binario, todo lo que tenemos que hacer es cambiar cada bit por turno. Por lo tanto, el complemento a uno de «1» es «0» y viceversa, entonces el complemento a uno de 10010100₂ es simplemente 01101011₂ ya que todos los 1 se cambian a 0 y los 0 a 1.

La forma más fácil de encontrar el complemento a uno de un número binario con signo cuando se construyen circuitos decodificadores lógicos o aritméticos digitales es utilizar inversores. El inversor es naturalmente un generador de complemento y se puede usar en paralelo para encontrar el complemento a 1 de cualquier número binario como se muestra:

Complemento de 1 usando inversores

Entonces podemos ver que es muy fácil encontrar el complemento a uno de un número binario N, ya que todo lo que necesitamos hacer es simplemente cambiar los 1 por 0 y los 0 por 1 para darnos un -N equivalente. Además, al igual que la representación anterior de magnitud de signo, el complemento de uno también puede tener notación de n bits para representar números en el rango de: -2^(n-1)  y  +2^(n-1) – 1. Por ejemplo, una representación de 4 bits en formato de complemento a uno se puede utilizar para representar números decimales en el rango de -7 a +7 con dos representaciones de cero: 0000 (+0) y 1111 (-0) igual que antes.

Suma y resta usando el complemento a uno

Una de las principales ventajas del complemento a uno es la suma y resta de dos números binarios. En matemáticas, la resta se puede implementar en una variedad de formas diferentes como A – B, es lo mismo que decir A + (-B) o -B + A, etc. Por lo tanto, la complicación de restar dos números binarios se puede realizar simplemente usando la suma.

Vimos en el tutorial de sumador binario que la suma binaria sigue las mismas reglas que la suma normal, excepto que en binario solo hay dos bits (dígitos) y el dígito más grande es un «1», (al igual que el «9» es el más grande dígito decimal) por lo tanto, las combinaciones posibles para la suma binaria son las siguientes:

0	0	1	1
+ 0	+ 1	+ 0	+ 1
0	1	1	1 ← 0	(0 más un acarreo 1)

Cuando los dos números a sumar son ambos positivos, la suma A + B, se pueden sumar mediante la suma directa (incluyendo el número y el signo de bit), porque cuando se suman bits individuales, “0 + 0”, “0 + 1” o “1 + 0” resulta en una suma de “0” o “1”. Esto se debe a que cuando los dos bits que queremos sumar son impares (“0” + “1” o “1 + 0”), el resultado es “1”. Del mismo modo, cuando los dos bits que se van a sumar son pares («0 + 0» o «1 + 1») el resultado es «0» hasta llegar a «1 + 1», entonces la suma es igual a «0» más un llevar «1». Veamos un ejemplo sencillo.

Resta de dos números binarios

Se requiere un sistema digital de 8 bits para restar los siguientes dos números 115 y 27 utilizando el complemento a uno. Entonces, en decimal, esto sería: 115 – 27 = 88.

Primero necesitamos convertir los dos números decimales en binarios y asegurarnos de que cada número tenga el mismo número de bits agregando ceros a la izquierda para producir un número de 8 bits (byte). Por lo tanto:

115₁₀  en binario es: 01110011₂

27₁₀   en binario es: 00011011₂

Ahora necesitamos encontrar el complemento del segundo número binario, (00011011) dejando el primer número (01110011) sin cambios. Entonces, al cambiar todos los 1 por 0 y los 0 por 1, el complemento a uno de 00011011 es, por lo tanto, igual a 11100100.

Sumando el primer número y el complemento del segundo número da:

01110011

+ 11100100

Desbordamiento → 1 01010111

Dado que el sistema digital debe trabajar con 8 bits, solo se utilizan los primeros ocho dígitos para proporcionar la respuesta a la suma, y ​​simplemente ignoramos el último bit (bit 9). Este bit se denomina bit de «desbordamiento». El desbordamiento ocurre cuando la suma de la columna más significativa (más a la izquierda) produce un arrastre. Este bit de desbordamiento o acarreo se puede ignorar por completo o pasar a la siguiente sección digital para usarlo en sus cálculos. El desbordamiento indica que la respuesta es positiva, si no hay desbordamiento, la respuesta es negativa.

El resultado de 8 bits de arriba es: 01010111 (el desbordamiento «1» se cancela) y para convertirlo de la respuesta de complemento a uno a la respuesta real, ahora tenemos que agregar «1» al resultado del complemento a uno, por lo tanto:

01010111

+ 1

01011000

Entonces, el resultado de restar 27 ( 00011011₂ ) de 115 ( 01110011₂ ) usando el complemento de 1 en binario da la respuesta de: 01011000₂ o (64 + 16 + 8) = 88₁₀ en decimal.

Luego, podemos ver que los números binarios con o sin signo se pueden restar entre sí utilizando el complemento de uno y el proceso de suma. Los sumadores binarios como el TTL 74LS83 o 74LS283 se pueden usar para sumar o restar dos números binarios con signo de 4 bits o en cascada para producir sumadores de 8 bits completos con la ejecución.

El complemento a dos en un número binario con signo

El complemento a dos con signo, es otro método como la forma de signo-magnitud anterior y el complemento a uno, que podemos usar para representar números binarios negativos en un sistema numérico binario con signo. En complemento a dos, los números positivos son exactamente los mismos que antes para los números binarios sin signo. Sin embargo, un número negativo está representado por un número binario, que cuando se suma a su correspondiente equivalente positivo resulta en cero.

En forma de complemento a dos, un número negativo es el complemento a 2 de su número positivo con la resta de dos números siendo A – B = A + (complemento a 2 de B) usando prácticamente el mismo proceso que antes, ya que básicamente, el complemento a dos es el complemento a uno + 1.

La principal ventaja del complemento a dos sobre el complemento a uno anterior es que no hay problema de doble cero y es mucho más fácil generar el complemento a dos de un número binario con signo. Por lo tanto, las operaciones aritméticas son relativamente más fáciles de realizar cuando los números se representan en formato de complemento a dos.

Veamos la resta de nuestros dos números de 8 bits 115 y 27 de arriba usando el complemento a dos, y recordamos de arriba que los equivalentes binarios son:

115₁₀  en binario es: 01110011₂

27₁₀   en binario es: 00011011₂

Nuestros números tienen 8 bits de longitud, entonces hay 2⁸ dígitos disponibles para representar nuestros valores y en binario esto es igual a: 100000000₂ o 256₁₀. Entonces el complemento a dos de 27₁₀ será:

(2⁸)₂ – 00011011 = 100000000 – 00011011 = 11100101₂

La complementación del segundo número negativo significa que la resta se convierte en una suma mucho más fácil de los dos números, por lo que la suma es: 115 + (complemento a 2 de 27) que es:

01110011 + 11100101 = 1 01011000₂

Como anteriormente, el noveno bit de desbordamiento no se tiene en cuenta ya que solo nos interesan los primeros 8 bits, por lo que el resultado es: 01011000₂ o (64 + 16 + 8) = 88₁₀ en decimal igual que antes.

Resumen de números binarios con signo

Hemos visto que los números binarios negativos se pueden representar utilizando el bit más significativo (MSB) como bit de signo. Si un n bits número binario detiene signo, el bit más a la izquierda se usa para representar el signo, dejando n-1 bits para representar el número.

Por ejemplo, en un número binario de 4 bits, esto deja solo 3 bits para contener el número real. Sin embargo, si el número binario no tiene signo, todos los bits se pueden usar para representar el número.

La representación de un número binario con signo se denomina comúnmente notación de magnitud de signo y si el bit de signo es «0», el número es positivo. Si el bit de signo es «1», entonces el número es negativo. Cuando se trata de operaciones aritméticas binarias, es más conveniente utilizar el complemento del número negativo.

La complementación es una forma alternativa de representar números binarios negativos. Este sistema de codificación alternativo permite la resta de números negativos mediante la suma simple.

Dado que los números de magnitud de signo positivo siempre comienzan con un cero (0), su complemento, por lo tanto, siempre comenzará con un uno (1) para indicar un número negativo como se muestra en la siguiente tabla.

Comparación de números binarios con signo de 4 bits

Decimal	Magnitud con signo	Complemento uno con signo	Complemento dos con signo
+7	0111	0111	0111
+6	0110	0110	0110
+5	0101	0101	0101
+4	0100	0100	0100
+3	0011	0011	0011
+2	0010	0010	0010
+1	0001	0001	0001
0	0000	0000	0000
-0	1000	1111	–
-1	1001	1110	1111
-2	1010	1101	1110
-3	1011	1100	1101
-4	1.100	1.011	1.100
-5	1.101	1.010	1.011
-6	1.110	1.001	1.010
-7	1111	1000	1001

Las formas del complemento firmado de números binarios puede usar complemento de 1 o complemento de 2. El complemento a 1 y el complemento a 2 de un número binario son importantes porque permiten la representación de números negativos.

El método de la aritmética en complemento a 2 se usa comúnmente en computadoras para manejar números negativos, la única desventaja es que si queremos representar números binarios negativos en el formato de número binario con signo, debemos renunciar a parte del rango del número positivo que teníamos antes.