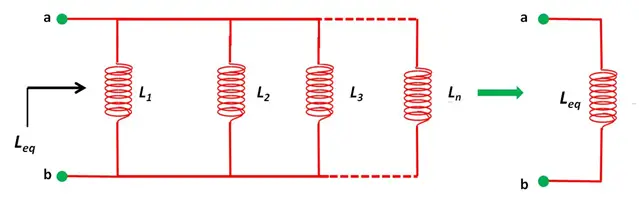
Se consideran inductores en paralelo cuando ambos terminales están conectados respectivamente a cada terminal de otro inductor o inductores.
La caída de voltaje en todos los inductores en paralelo será la misma. Entonces, los inductores en paralelo tienen un voltaje común a través de ellos y en nuestro ejemplo a continuación, el voltaje a través de los inductores se da como:
VL1 = VL2 = VL3 = VAB … etc.
En el siguiente circuito de los inductores L1, L2 y L3 están todos conectados entre sí en paralelo entre los dos puntos A y B.
Contenido
Inductores en circuito paralelo

En el tutorial de inductores de la serie anterior, vimos que la inductancia total, LT del circuito era igual a la suma de todos los inductores individuales sumados. Para inductores en paralelo, la inductancia del circuito equivalente LT se calcula de manera diferente.
La suma de las corrientes individuales que fluyen a través de cada inductor se puede encontrar usando la Ley de Corriente de Kirchoff (KCL) donde, IT = I1 + I2 + I3 y sabemos por los tutoriales anteriores sobre inductancia que la fem autoinducida a través de un inductor se da como: V = L di / dt
Luego, tomando los valores de las corrientes individuales que fluyen a través de cada inductor en nuestro circuito anterior, y sustituyendo la corriente i por i1 + i2 + i3, el voltaje a través de la combinación en paralelo es dado como:

Sustituyendo di / dt en la ecuación anterior con v / L da:

Podemos reducirlo para dar una expresión final para calcular la inductancia total de un circuito cuando se conectan inductores en paralelo y esto se da como:
Ecuación del inductor paralelo

Aquí, al igual que los cálculos para resistencias en paralelo, el valor recíproco ( 1 / Ln ) de las inductancias individuales se suman todas juntas en lugar de las inductancias mismas. Pero de nuevo, como ocurre con las inductancias conectadas en serie, la ecuación anterior sólo es cierta cuando hay inductancia mutua «NO» o acoplamiento magnético entre dos o más de los inductores (están magnéticamente aislados entre sí). Cuando hay acoplamiento entre bobinas, la inductancia total también se ve afectada por la cantidad de acoplamiento.
Este método de cálculo se puede utilizar para calcular cualquier número de inductancias individuales conectadas entre sí dentro de una sola red en paralelo. Sin embargo, si solo hay dos inductores individuales en paralelo, entonces se puede usar una fórmula mucho más simple y rápida para encontrar el valor de inductancia total, y esto es:

Un punto importante para recordar acerca de los inductores en circuitos en paralelo, la inductancia total ( LT ) de dos o más inductores conectados entre sí en paralelo siempre será MENOR que el valor de la inductancia más pequeña en la cadena paralela.
Ejemplo de Inductores en paralelo No.1
Tres inductores de 60 mH, 120 mH y 75 mH, respectivamente, están conectados entre sí en una combinación en paralelo sin inductancia mutua entre ellos. Calcule la inductancia total de la combinación en paralelo en milihenries.

Inductores mutuamente acoplados en paralelo
Cuando los inductores están conectados entre sí en paralelo de modo que el campo magnético de uno se vincula con el otro, el efecto de la inductancia mutua aumenta o disminuye la inductancia total dependiendo de la cantidad de acoplamiento magnético que existe entre las bobinas. El efecto de esta inductancia mutua depende de la distancia entre las bobinas y su orientación entre sí.
Los inductores conectados mutuamente en paralelo se pueden clasificar como «auxiliares» u «opuestos» a la inductancia total con bobinas conectadas auxiliares en paralelo que aumentan la inductancia equivalente total y bobinas opuestas en paralelo que disminuyen la inductancia equivalente total en comparación con las bobinas que tienen inductancia mutua cero.
Las bobinas paralelas acopladas mutuamente se pueden mostrar conectadas en una configuración auxiliar o opuesta mediante el uso de puntos de polaridad o marcadores de polaridad como se muestra a continuación.
Inductores auxiliares paralelos

El voltaje a través de los dos inductores auxiliares en paralelo anteriores debe ser igual, ya que están en paralelo, por lo que las dos corrientes, i1 e i2 deben variar para que el voltaje entre ellos permanezca igual. Entonces, la inductancia total, LT para dos inductores auxiliares paralelos se da como:

Donde: 2M representa la influencia de la bobina L 1 sobre L 2 e igualmente la bobina L 2 sobre L 1.
Si las dos inductancias son iguales y el acoplamiento magnético es perfecto tal como en un circuito toroidal, entonces la inductancia equivalente de los dos inductores en paralelo es L como LT = L1 = L2 =M. Sin embargo, si la inductancia mutua entre ellos es cero, la inductancia equivalente sería L ÷ 2 igual que para dos inductores autoinducidos en paralelo.
Si una de las dos bobinas se invirtiera con respecto a la otra, entonces tendríamos dos inductores opuestos paralelos y la inductancia mutua, M que existe entre las dos bobinas tendrá un efecto de cancelación en cada bobina en lugar de un efecto de ayuda como se muestra a continuación.
Inductores opuestos paralelos

Entonces, la inductancia total, LT para dos inductores opuestos en paralelo se da como:

Esta vez, si las dos inductancias tienen el mismo valor y el acoplamiento magnético es perfecto entre ellas, la inductancia equivalente y también la fem autoinducida a través de los inductores será cero, ya que los dos inductores se cancelan entre sí.
Esto se debe a que a medida que las dos corrientes, i1 e i2 fluyen a través de cada inductor, el flujo mutuo total generado entre ellos es cero porque los dos flujos producidos por cada inductor son iguales en magnitud pero en direcciones opuestas.
Luego, las dos bobinas se convierten efectivamente en un cortocircuito al flujo de corriente en el circuito, por lo que la inductancia equivalente, LT, se vuelve igual a (L ± M) ÷ 2.
Ejemplo de Inductores en paralelo No.2
Dos inductores cuyas autoinductancias son de 75 mH y 55 mH respectivamente están conectados entre sí en ayuda de paralelo. Su inductancia mutua es de 22,5 mH. Calcule la inductancia total de la combinación en paralelo.

Ejemplo de Inductores en paralelo No.3
Calcule la inductancia equivalente del siguiente circuito inductivo.

Calcule la primera rama del inductor LA, (inductor L5 en paralelo con los inductores L6 y L7)

Calcule la segunda rama del inductor LB, (Inductor L3 en paralelo con los inductores L4 y LA)

Calcule la inductancia del circuito equivalente LEQ, (inductor L1 en paralelo con los inductores L2 y LB)

Entonces se encontró que la inductancia equivalente para el circuito anterior era: 15 mH.
Resumen de Inductores en paralelo
Al igual que con la resistencia, los inductores conectados entre sí en paralelo tienen el mismo voltaje, V a través de ellos. Además, conectar inductores en paralelo disminuye la inductancia efectiva del circuito, siendo la inductancia equivalente de “N” inductores conectados en paralelo el recíproco de la suma de los recíprocos de las inductancias individuales.
Al igual que con los inductores conectados en serie, los inductores conectados mutuamente en paralelo se clasifican como «auxiliares» u «opuestos» a esta inductancia total dependiendo de si las bobinas están acopladas acumulativamente (en la misma dirección) o acopladas diferencialmente (en la dirección opuesta).
Hasta ahora hemos examinado el inductor como un componente pasivo puro o ideal. En el próximo tutorial sobre inductores, veremos inductores no ideales que tienen bobinas resistivas del mundo real que producen el circuito equivalente de un inductor en serie con una resistencia y examinaremos la constante de tiempo de dicho circuito.