Todas las bobinas, inductores, inductores y transformadores crean un campo magnético a su alrededor y consisten en una inductancia en serie con una resistencia que forma un circuito serie LR.
El primer tutorial en esta sección sobre inductores, analizamos brevemente la constante de tiempo de un inductor indicando que la corriente que fluye a través de un inductor no podría cambiar instantáneamente, sino que aumentaría a una tasa constante determinada por la fem autoinducida en el inductor.
En otras palabras, un inductor en un circuito eléctrico se opone al flujo de corriente, (i) a través de él. Si bien esto es perfectamente correcto, asumimos en el tutorial que era un inductor ideal que no tenía resistencia o capacitancia asociada con los devanados de su bobina.
Sin embargo, en el mundo real, “TODAS” las bobinas, ya sean estranguladores, solenoides, relés o cualquier componente de la herida, siempre tendrán una cierta cantidad de resistencia, sin importar cuán pequeña sea. Esto se debe a que las bobinas reales de alambre que se utilizan para hacerlas usan alambre de cobre que tiene un valor resistivo.
A continuación, los efectos del mundo real que podemos considerar nuestra bobina simple como ser una “inductancia” L, en serie con una “resistencia” R. En otras palabras, formando un circuito serie LR.
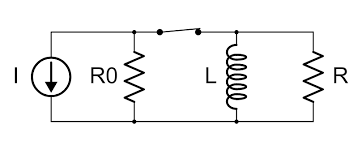
Un circuito serie LR consiste básicamente en un inductor de inductancia, L conectado en serie con un resistor de resistencia, R. La resistencia «R» es el valor resistivo de CC de las vueltas o bucles del cable que forman la bobina de los inductores. Considere el circuito serie LR a continuación:
Contenido
El circuito serie LR

El anterior circuito serie LR está conectado a través de una fuente de voltaje constante (la batería) y un interruptor. Suponga que el interruptor, S está abierto hasta que se cierra en un tiempo t = 0, y luego permanece permanentemente cerrado produciendo una entrada de voltaje de tipo «respuesta escalonada». La corriente, i comienza a fluir a través del circuito, pero no aumenta rápidamente a su valor máximo de Imax según lo determinado por la relación de V / R (Ley de Ohm).
Este factor limitante se debe a la presencia de fem autoinducida dentro del inductor como resultado del crecimiento del flujo magnético (Ley de Lenz). Después de un tiempo, la fuente de voltaje neutraliza el efecto de la fem autoinducida, el flujo de corriente se vuelve constante y la corriente y el campo inducidos se reducen a cero.
Podemos usar la Ley de voltaje de Kirchhoff, (KVL) para definir las caídas de voltaje individuales que existen alrededor del circuito y luego, con suerte, usarla para darnos una expresión para el flujo de corriente.
La ley de voltaje de Kirchhoff (KVL) nos da:

La caída de voltaje a través de la resistencia, R es I * R (Ley de Ohm).

La caída de voltaje a través del inductor, L es ahora nuestra expresión familiar L (di / dt)

Entonces, la expresión final para las caídas de voltaje individuales alrededor del circuito en serie LR se puede dar como:

Podemos ver que la caída de voltaje a través de la resistencia depende de la corriente, i, mientras que la caída de voltaje a través del inductor depende de la tasa de cambio de la corriente, di / dt. Cuando la corriente es igual a cero, ( i = 0 ) en el tiempo t = 0, la expresión anterior, que también es una ecuación diferencial de primer orden, puede reescribirse para dar el valor de la corriente en cualquier instante de tiempo como:
Expresión para la corriente en un circuito serie LR

- Donde:
- V está en voltios
- R está en ohmios
- L está en Henries
- t es en segundos
- e es la base del logaritmo natural = 2.71828
La constante de tiempo, ( τ ) del circuito serie LR se da como L / R y en la que V / R representa el valor final de la corriente en estado estable después de cinco valores de constantes de tiempo. Una vez que la corriente alcanza este valor máximo de estado estable en 5τ, la inductancia de la bobina se ha reducido a cero actuando más como un cortocircuito y eliminándola efectivamente del circuito.
Por lo tanto, la corriente que fluye a través de la bobina está limitada sólo por el elemento resistivo en ohmios de los devanados de las bobinas. Se puede hacer una representación gráfica del crecimiento de la corriente que representa las características de voltaje / tiempo del circuito como.
Curvas transitorias para un circuito serie LR

Dado que la caída de voltaje a través de la resistencia, VR es igual a I * R (Ley de Ohm), tendrá el mismo crecimiento y forma exponencial que la corriente. Sin embargo, la caída de voltaje a través del inductor, VL tendrá un valor igual a: Ve(-Rt / L). Entonces, el voltaje a través del inductor, VL , tendrá un valor inicial igual al voltaje de la batería en el momento t = 0 o cuando el interruptor se cierra por primera vez y luego decae exponencialmente a cero como se representa en las curvas anteriores.
El tiempo requerido para que la corriente que fluye en el circuito serie LR alcance su valor máximo de estado estable es equivalente a aproximadamente 5 constantes de tiempo o 5τ. Esta constante de tiempo τ, se mide por τ = L / R, en segundos, donde R es el valor de la resistencia en ohmios y L es el valor del inductor en Henries. Esto entonces forma la base de un circuito de carga RL donde 5τ también se puede considerar como “5 * (L / R)” o el tiempo transitorio del circuito.
El tiempo transitorio de cualquier circuito inductivo está determinado por la relación entre la inductancia y la resistencia. Por ejemplo, para una resistencia de valor fijo, cuanto mayor sea la inductancia, más lento será el tiempo transitorio y, por lo tanto, una constante de tiempo más larga para el circuito serie LR. Asimismo, para una inductancia de valor fijo, cuanto menor es el valor de resistencia, mayor es el tiempo transitorio.
Sin embargo, para una inductancia de valor fijo, al aumentar el valor de resistencia, el tiempo transitorio y, por lo tanto, la constante de tiempo del circuito se acorta. Esto se debe a que a medida que aumenta la resistencia, el circuito se vuelve cada vez más resistivo a medida que el valor de la inductancia se vuelve insignificante en comparación con la resistencia. Si el valor de la resistencia aumenta lo suficiente en comparación con la inductancia, el tiempo transitorio se reduciría efectivamente a casi cero.
Ejemplo de circuito serie LR No.1
Se conecta una bobina que tiene una inductancia de 40 mH y una resistencia de 2Ω para formar un circuito en serie LR. Si están conectados a una fuente de 20 V CC.
a). ¿Cuál será el valor final de estado estable de la corriente?

b) ¿Cuál será la constante de tiempo del circuito en serie RL?

c) ¿Cuál será el tiempo transitorio del circuito serie RL?

d) ¿Cuál será el valor de la fem inducida después de 10 ms?

e) ¿Cuál será el valor de la corriente del circuito una vez constante después de que se cierre el interruptor?

La constante de tiempo, τ del circuito se calculó en la pregunta b) como 20 ms. Entonces la corriente del circuito en este momento se da como:

Es posible que haya notado que la respuesta para la pregunta (e), que da un valor de 6.32 amperios en una constante de tiempo, es igual al 63.2% del valor final de corriente de estado estable de 10 amperios que calculamos en la pregunta (a). Este valor de 63,2% o 0,632 x IMAX también se corresponde con las curvas transitorias que se muestran arriba.
Energía en un circuito serie LR
Luego, desde arriba, la tasa instantánea a la que la fuente de voltaje entrega energía al circuito se da como:

La velocidad instantánea a la que la resistencia disipa la potencia en forma de calor se da como:

La velocidad a la que se almacena energía en el inductor en forma de energía potencial magnética se da como:

Entonces podemos encontrar la potencia total en un circuito serie RL multiplicando por i y es por lo tanto:

Donde el primer término I2R representa la potencia disipada por la resistencia en calor, y el segundo término representa la potencia absorbida por el inductor, su energía magnética.