Voltaje nodal

El análisis de voltaje nodal complementa el análisis de malla anterior en que es igualmente poderoso y se basa en los mismos conceptos de matriz análisis. Como su nombre lo indica, el análisis de voltaje nodal utiliza las ecuaciones «nodales» de la primera ley de Kirchhoff para encontrar los potenciales de voltaje alrededor del circuito.

Entonces, al sumar todos estos voltajes nodales, el resultado neto será igual a cero. Entonces, si hay «n» nodos en el circuito, habrá «n-1» ecuaciones nodales independientes y estas por sí solas son suficientes para describir y, por lo tanto, resolver el circuito.

En cada punto del nodo, escriba la primera ecuación de la ley de Kirchhoff, es decir: “las corrientes que entran en un nodo son exactamente iguales en valor a las corrientes que salen del nodo” y luego exprese cada corriente en términos del voltaje a través de la rama. Para “n” nodos, un nodo se utilizará como nodo de referencia y todos los demás voltajes serán referenciados o medidos con respecto a este nodo común.

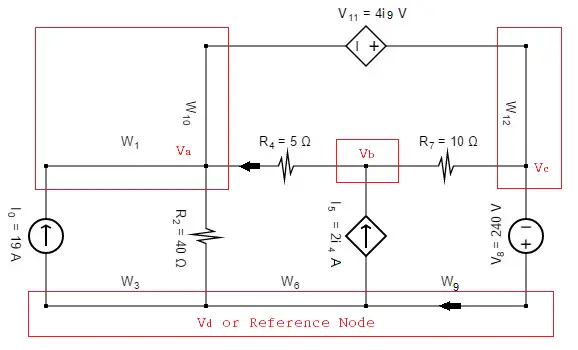
Por ejemplo, considere el circuito de la sección anterior.

Análisis de circuito de voltaje nodal

En el circuito anterior, el nodo D se elige como el nodo de referencia y los otros tres nodos se supone que tienen voltajes, Va, Vb y Vc con respecto al nodo D. Por ejemplo:

Como Va = 10v y Vc = 20v , Vb se puede encontrar fácilmente mediante:

Nuevamente es el mismo valor de 0.286 amperios, que encontramos usando la Ley de Circuitos de Kirchhoff en el tutorial anterior.

De los métodos de análisis de malla y nodal que hemos analizado hasta ahora, este es el método más simple para resolver este circuito en particular. Generalmente, el análisis de voltaje nodal es más apropiado cuando hay un mayor número de fuentes de corriente alrededor. Entonces, la red se define como: [ I ] = [ Y ] [ V ] donde [ I ] son ​​las fuentes de corriente de conducción, [ V ] son ​​los voltajes nodales que se encontrarán y [ Y ] es la matriz de admitancia de la red que opera en [ V ] para dar [ I ].

Resumen del análisis de voltaje nodal.

El procedimiento básico para resolver las ecuaciones del análisis de voltaje nodal es el siguiente:

• 1. Escriba los vectores de corriente, asumiendo que las corrientes en un nodo son positivas. Es decir, (N x 1) matrices para «N» nodos independientes.
• 2. Escriba la matriz de admitancia [Y] de la red donde:
  •   Y11 = la admisión total del primer nodo.
  •   Y22 = la admisión total del segundo nodo.
  •   RJK = la admitancia total de unirse el nodo J al nodo K.
• 3. Para una red con “N” nodos independientes, [Y] será una matriz (N x N) y que Ynn será positivo y Yjk será negativo o valor cero.
• 4. El vector de voltaje será (N x L) y enumerará los voltajes “N” que se encontrarán.

Ahora hemos visto que existen varios teoremas que simplifican el análisis de circuitos lineales. En el siguiente tutorial veremos el Teorema de Thevenin, que permite representar una red que consta de resistencias y fuentes lineales mediante un circuito equivalente con una sola fuente de voltaje y una resistencia en serie.