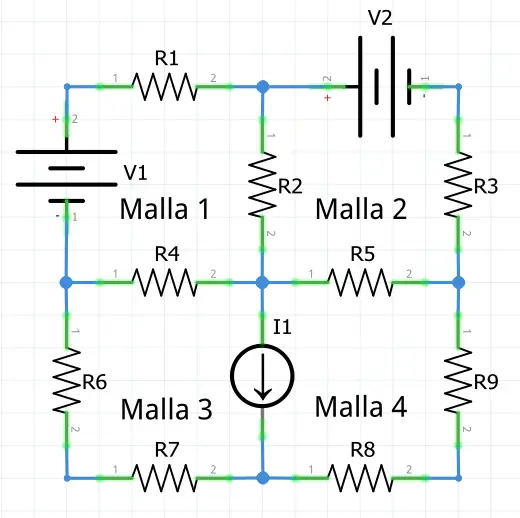
Método de corriente de mallas de Kirchhoff

Si bien las leyes de Kirchhoff nos brindan el método básico para analizar cualquier circuito eléctrico complejo, existen diferentes formas de mejorar este método mediante el uso del análisis de la corriente de mallas o el análisis de voltaje nodal que resulta en una disminución de las matemáticas involucradas y cuando hay grandes redes involucradas, esta reducción en matemáticas puede ser una gran ventaja.

Por ejemplo, considere el ejemplo de circuito eléctrico de la sección anterior.

Análisis del circuito de la corriente de mallas

Un método simple para reducir la cantidad de matemáticas involucradas es analizar el circuito usando las ecuaciones de la Ley de Corriente de Kirchhoff para determinar las corrientes, I1 y I2 fluyendo en las dos resistencias. Entonces no hay necesidad de calcular la corriente I3 ya que es solo la suma de I1 y yo2. Entonces, la segunda ley de voltaje de Kirchhoff simplemente se convierte en:

• Ecuación No    1 :10 = 50I1 + 40I2
• Ecuación No    2 :20 = 40I1 + 60I2

Por lo tanto, se ha guardado una línea de cálculo matemático.

Análisis de la corriente de malla

Un método más fácil de resolver el circuito anterior es mediante el análisis de la corriente de malla o el análisis de bucle, que a veces también se denomina método de corrientes circulantes de Maxwell. En lugar de etiquetar las corrientes derivadas, debemos etiquetar cada «bucle cerrado» con una corriente circulante.

Como regla general, solo etiquete los bucles internos en el sentido de las agujas del reloj con corrientes circulantes, ya que el objetivo es cubrir todos los elementos del circuito al menos una vez. Cualquier corriente de derivación requerida se puede encontrar a partir del lazo apropiado o las corrientes de malla como antes usando el método de Kirchhoff.

Por ejemplo:    i1 = I1 , i2 = -I2  y  I3 = I1 – I2

Ahora escribimos la ecuación de la ley de voltaje de Kirchhoff de la misma manera que antes para resolverlos, pero la ventaja de este método es que asegura que la información obtenida de las ecuaciones del circuito sea la mínima requerida para resolver el circuito, ya que la información es más general y se puede poner fácilmente en forma de matriz.

Por ejemplo, considere el circuito de la sección anterior.

Estas ecuaciones se pueden resolver con bastante rapidez mediante el uso de una única malla matriz  de impedancia Z. Cada elemento de la diagonal principal será «positivo» y es la impedancia total de cada malla. Donde, como, cada elemento fuera de la diagonal principal será «cero» o «negativo» y representa el elemento del circuito que conecta todas las mallas apropiadas.

Primero, debemos entender que cuando se trata de matrices, para la división de dos matrices es lo mismo que multiplicar una matriz por la inversa de la otra como se muestra:

Habiendo encontrado la inversa de R, ya que V / R es lo mismo que V x R-1, ahora podemos usarlo para encontrar las dos corrientes circulantes.

Donde:

• [V]   da el voltaje total de la batería para el lazo 1 y luego el lazo 2
• [I]     indica los nombres de las corrientes de lazo que estamos tratando de encontrar
• [R]   es la matriz de resistencia
• [R-1 ]   es la inversa de la [R] matriz

Y esto da I1 como -0,143 amperios e I2 como -0,429 amperios

Como:    I3 = I1 – I2

Por lo tanto, la corriente combinada de I3 se da como:   -0,143 – (-0,429) = 0,286 Amperios

Este es el mismo valor de  0.286 amperios de corriente, que encontramos anteriormente en el tutorial de ley de circuitos de Kirchhoff.

Resumen del análisis de mallas de Kirchhoff

Este método de análisis de circuito de “mirar-ver” es probablemente el mejor de todos los métodos de análisis de circuito con el procedimiento básico para resolver ecuaciones, considere lo siguiente:

• 1. Etiquete todos los lazos internos con corrientes circulantes. (I1, I2,… IL, etc.)
• 2. Escriba la[ L x 1 matriz de columnas] [ V ] dando la suma de todas las fuentes de voltaje en cada lazo.
• 3. Escriba la[ L x L matriz], [ R ] para todas las resistencias en el circuito de la siguiente manera:
  •   R11 = la resistencia total en el primer bucle.
  •   Rnn = la resistencia total en el N-ésimo bucle.
  •   RJK = la resistencia que une directamente el bucle J con el bucle K.
• 4. Escriba la matriz o ecuación vectorial [V] = [R] x [I] donde [I] es la lista de corrientes que se encontrarán.

Además de usar el análisis de mallas, también podemos usar el análisis de nodos para calcular los voltajes alrededor de los bucles, lo que nuevamente reduce la cantidad de matemáticas requeridas usando solo las leyes de Kirchoff. En el siguiente tutorial relacionado con la teoría de circuitos de CC, veremos el Análisis de voltaje nodal para hacer precisamente eso.