Teorema de Norton

El teorema de Norton establece que “cualquier circuito lineal que contenga varias fuentes de energía y resistencias puede ser reemplazado por un solo generador de corriente constante en paralelo con una sola resistencia”.

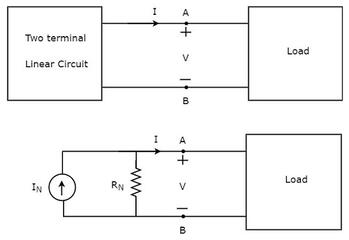
En lo que respecta a la resistencia de carga, RL se refiere a esta resistencia única, RS es el valor de la resistencia mirando hacia atrás en la red con todas las fuentes de corriente en circuito abierto e IS es la corriente de cortocircuito en los terminales de salida como se muestra a continuación:

Circuito equivalente de Norton

El valor de esta «corriente constante» es el que fluirá si las dos terminales de salida estuvieran en cortocircuito, mientras que la resistencia de la fuente se mediría mirando hacia atrás en las terminales (lo mismo que Thevenin).

Por ejemplo, considere nuestro circuito ahora familiar de la sección anterior:

Para encontrar el circuito equivalente de Norton del circuito anterior, primero tenemos que quitar la central de 40Ω de resistencia a la carga y cortocircuitar las terminales A y B para darnos el siguiente circuito:

Cuando los terminales A y B están en cortocircuito, las dos resistencias están conectadas en paralelo a través de sus dos fuentes de voltaje respectivas y las corrientes que fluyen a través de cada resistencia, así como la corriente total de cortocircuito ahora se puede calcular como:

Con AB en cortocircuito

Si cortocircuitamos las dos fuentes de voltaje y los terminales de circuito abierto A y B, las dos resistencias ahora están efectivamente conectadas juntas en paralelo. El valor de la resistencia interna Rs se encuentra calculando la resistencia total en los terminales A y B, lo que nos da el siguiente circuito:

Encuentre la resistencia equivalente (Rs)

Habiendo encontrado tanto la corriente de cortocircuito, Is como la resistencia interna equivalente, Rs esto nos da el siguiente circuito equivalente de Norton:

Circuito equivalente de Norton

Hasta ahora todo bien, pero ahora tenemos que resolver con la original de 40Ω de resistencia de la carga conectada a los terminales A y B como se muestra a continuación:

Nuevamente, las dos resistencias están conectadas en paralelo a través de los terminales A y B, lo que nos da una resistencia total de:

El voltaje a través de los terminales A y B con la resistencia de carga conectada se da como:

Entonces, la corriente que fluye en la 40Ω de resistencia de la carga, se puede encontrar como:

Una vez más y usando el teorema de Norton, el valor de la corriente para I3 aún se calcula como 0.286 amperios, que encontramos usando la ley de circuito de Kirchhoff en los tutoriales anteriores.

Resumen del teorema de Norton

El procedimiento básico para resolver un circuito usando el teorema de Norton es el siguiente:

• 1. Retire la resistencia de carga RL o el componente en cuestión.
• 2. Encuentre RS cortocircuitando todas las fuentes de voltaje o abriendo el circuito de todas las fuentes de corriente.
• 3. Encuentre IS mediante la colocación de un enlace de cortocircuito en los terminales de salida A y B.
• 4. Encontrar la corriente que fluye a través de la resistencia de carga RL.

En un circuito, la potencia suministrada a la carga es máxima cuando la resistencia de la carga es igual a la resistencia de la fuente. En el siguiente tutorial veremos la transferencia de potencia máxima. La aplicación del teorema de transferencia de potencia máxima se puede aplicar a circuitos lineales simples y complicados que tienen una carga variable y se utiliza para encontrar la resistencia de carga que conduce a la transferencia de la potencia máxima a la carga.