Resonancia en serie

Hasta ahora hemos analizado el comportamiento de un circuito en serie RLC cuya fuente de voltaje es un suministro sinusoidal de estado estable de frecuencia fija. También hemos visto en nuestro tutorial sobre circuitos en serie RLC que se pueden combinar dos o más señales sinusoidales utilizando fasores siempre que tengan el mismo suministro de frecuencia.

Pero, ¿qué pasaría con las características del circuito si se aplicara al circuito una tensión de alimentación de amplitud fija pero de diferentes frecuencias? Además, ¿cuál sería el comportamiento de la «respuesta de frecuencia» de los circuitos sobre los dos componentes reactivos debido a esta frecuencia variable?

En un circuito en serie RLC, se convierte en un punto de frecuencia donde la reactancia inductiva del inductor se vuelve igual en valor a la reactancia capacitiva del capacitor. En otras palabras, XL = XC. El punto en el que esto ocurre se denomina frecuencia de punto de resonancia del circuito (fr), y como estamos analizando un circuito en serie RLC esta frecuencia de resonancia produce una resonancia en serie.

La resonancia en serie de circuitos son uno de los circuitos eléctricos y electrónicos más importantes utilizados. Se pueden encontrar en diversas formas, como filtros de red de CA, filtros de ruido y también en circuitos de sintonización de radio y televisión que producen un circuito de sintonización muy selectivo para la recepción de los diferentes canales de frecuencia. Considere el circuito en serie RLC simple a continuación:

Circuito en serie RLC

En primer lugar, definamos lo que ya sabemos sobre los circuitos en serie RLC.

A partir de la ecuación anterior para la reactancia inductiva, si frecuencia o la inductancia, se aumenta el valor de la reactancia inductiva general del inductor también aumentaría. A medida que la frecuencia se acerca al infinito, la reactancia de los inductores también aumentaría hacia el infinito con el elemento del circuito actuando como un circuito abierto.

Sin embargo, a medida que la frecuencia se acerca a cero o CC, la reactancia de los inductores disminuiría a cero, provocando el efecto opuesto actuando como un cortocircuito. Esto significa entonces que la reactancia inductiva es «proporcional» a la frecuencia y es pequeña a bajas frecuencias y alta a frecuencias más altas y esto se demuestra en la siguiente curva:

Reactancia inductiva contra frecuencia

La gráfica de reactancia inductiva contra frecuencia es una curva lineal recta. El valor de reactancia inductiva de un inductor aumenta linealmente a medida que aumenta la frecuencia a través de él. Por lo tanto, la reactancia inductiva es positiva y es directamente proporcional a la frecuencia ( XL ∝ ƒ )

Lo mismo ocurre con la fórmula de reactancia capacitiva anterior, pero a la inversa. Si la frecuencia o la capacitancia aumenta, la reactancia capacitiva general disminuirá. A medida que la frecuencia se acerca al infinito, la reactancia de los condensadores se reduciría prácticamente a cero, lo que provocaría que el elemento del circuito actuará como un conductor perfecto de 0 Ω.

Pero a medida que la frecuencia se acerca a cero o al nivel de CC, la reactancia de los capacitores aumentaría rápidamente hasta el infinito, lo que haría que actuará como una resistencia muy grande, volviéndose más como una condición de circuito abierto. Esto significa entonces que la reactancia capacitiva es “inversamente proporcional” a la frecuencia para cualquier valor dado de capacitancia y esto se muestra a continuación:

Reactancia capacitiva contra frecuencia

La gráfica de reactancia capacitiva contra frecuencia es una curva hiperbólica. El valor de reactancia de un condensador tiene un valor muy alto a bajas frecuencias, pero disminuye rápidamente a medida que aumenta la frecuencia a través de él. Por tanto, la reactancia capacitiva es negativa e inversamente proporcional a la frecuencia ( XC ∝ ƒ -1 )

Podemos ver que los valores de estas resistencias dependen de la frecuencia del suministro. A una frecuencia más alta, XL es alta y a una frecuencia baja XC es alta. Entonces debe haber un punto de frecuencia donde el valor de XL es el mismo que el valor de XC y lo hay. Si ahora colocamos la curva de reactancia inductiva en la parte superior de la curva de reactancia capacitiva de modo que ambas curvas estén en los mismos ejes, el punto de intersección nos dará el punto de frecuencia de resonancia en serie, ( ƒr o ωr ) como se muestra a continuación:

Frecuencia de resonancia en serie

Donde: ƒr está en Hertz, L está en Henries y C está en Faradios.

La resonancia eléctrica se produce en un circuito de CA cuando los efectos de las dos reactancias, que son opuestas e iguales, se anulan entre sí como XL = XC. El punto en el gráfico anterior en el que esto sucede es donde las dos curvas de reactancia se cruzan. En un circuito resonante en serie, la frecuencia resonante, ƒr punto, se puede calcular de la siguiente manera:

Podemos ver entonces que en la resonancia, matemáticamente las dos reactancias se cancelan entre sí como XL – XC = 0. Esto hace que la combinación LC en serie actúe como un cortocircuito con la única oposición al flujo de corriente en un circuito de resonancia en serie siendo el resistencia, R.

En forma compleja, la frecuencia resonante es la frecuencia a la que la impedancia total de un circuito en serie RLC se vuelve puramente «real», es decir, no existen impedancias imaginarias. Esto se debe a que en la resonancia se cancelan. Así que la impedancia total del circuito en serie se convierte en sólo el valor de la resistencia y por lo tanto:  Z =R.

Luego, en la resonancia, la impedancia del circuito en serie está en su valor mínimo e igual solo a la resistencia, R del circuito. La impedancia del circuito en resonancia se denomina «impedancia dinámica» del circuito y, según la frecuencia, XC (normalmente a altas frecuencias) o XL (normalmente a bajas frecuencias) dominarán ambos lados de la resonancia como se muestra a continuación:

Impedancia en un circuito de resonancia en serie

Observe que cuando la reactancia capacitiva domina el circuito de la curva de impedancia tiene una forma hiperbólica a sí mismo, pero cuando la reactancia inductiva domina el circuito de la curva es no simétrica debido a la respuesta lineal de XL.

También puede notar que si la impedancia de los circuitos está en su mínimo en resonancia, entonces, en consecuencia, los circuitos de la admitancia deben estar en su máximo y una de las características de un circuito de resonancia en serie es que la admitancia es muy alta. Pero esto puede ser malo porque un valor muy bajo de resistencia en resonancia significa que la corriente resultante que fluye a través del circuito puede ser peligrosamente alta.

Recordamos desde el tutorial anterior sobre los circuitos serie RLC que el voltaje a través de una combinación serie es la suma vectorial de VR, VL y VC. Entonces, si en la resonancia las dos reactancias son iguales y cancelando, los dos voltajes que representan VL y VC también deben ser opuestos e iguales en valor, cancelando así entre sí porque con componentes puros los voltajes fasoriales se dibujan en +90° y -90° respectivamente.

Luego, en un circuito de resonancia en serie como VL = -VC, los voltajes reactivos resultantes son cero y todo el voltaje de suministro cae a través de la resistencia. Por lo tanto, VR = Vsuministro y es por esta razón que los circuitos de resonancia en serie se conocen como circuitos de resonancia de voltaje (a diferencia de los circuitos de resonancia en paralelo que son circuitos de resonancia de corriente).

Circuito de serie RLC en resonancia

Dado que la corriente que fluye a través de un circuito de resonancia en serie es el producto del voltaje dividido por la impedancia, en la resonancia la impedancia, Z está en su valor mínimo, ( = R ). Por lo tanto, la corriente del circuito a esta frecuencia estará en su valor máximo de V / R como se muestra a continuación:

Corriente de circuito en serie en resonancia

La curva de respuesta de frecuencia de un circuito de resonancia en serie muestra que la magnitud de la corriente es una función de la frecuencia y trazar esto en un gráfico nos muestra que la respuesta comienza cerca de cero, alcanza el valor máximo en la frecuencia de resonancia cuando IMAX = IR y luego vuelve a caer a casi cero cuando f se vuelve infinito. El resultado de esto es que las magnitudes de los voltajes a través del inductor, L y el capacitor, C pueden llegar a ser muchas veces mayores que el voltaje de suministro, incluso en resonancia, pero como son iguales y en oposición, se cancelan entre sí.

Como un circuito de resonancia en serie solo funciona en frecuencia resonante, este tipo de circuito también se conoce como circuito aceptor porque en resonancia, la impedancia del circuito está en su mínimo, por lo que acepta fácilmente la corriente cuya frecuencia es igual a su frecuencia resonante.

También puede notar que como la corriente máxima a través del circuito en resonancia está limitada sólo por el valor de la resistencia (un valor puro y real), el voltaje de la fuente y la corriente del circuito deben estar en fase entre sí a esta frecuencia. Entonces, el ángulo de fase entre el voltaje y la corriente de un circuito de resonancia en serie también es una función de la frecuencia para un voltaje de suministro fijo y que es cero en el punto de frecuencia de resonancia cuando: V, I y VR están todos en fase entre sí como mostrado a continuación. En consecuencia, si el ángulo de fase es cero, entonces el factor de potencia debe ser la unidad.

Ángulo de fase de un circuito de resonancia en serie

Observe también que el ángulo de fase es positivo para las frecuencias por encima de ƒr y negativo para las frecuencias por debajo de ƒr y esto se puede demostrar mediante:

Ancho de banda de un circuito de resonancia en serie

Si el circuito en serie RLC es impulsado por una frecuencia variable a un voltaje constante, entonces la magnitud de la corriente, I es proporcional a la impedancia, Z,por lo tanto, en la resonancia de la potencia absorbida por el circuito debe estar en su valor máximo como P = I2Z.

Si ahora reducimos o aumentamos la frecuencia hasta que la potencia promedio absorbida por la resistencia en el circuito de resonancia en serie sea la mitad de su valor máximo en resonancia, producimos dos puntos de frecuencia llamados puntos de media potencia que son -3dB por debajo del máximo, tomando 0dB como referencia de corriente máxima.

Estos puntos de -3dB nos dan un valor de corriente que es 70,7% de su valor máximo de resonancia que se define como: 0,5 (I2 R) = (0,707 x I)2 R. Entonces, el punto correspondiente a la frecuencia más baja a la mitad de la potencia se denomina «frecuencia de corte inferior», etiquetada como ƒL y el punto correspondiente a la frecuencia superior a la mitad de la potencia se denomina «frecuencia de corte superior», etiquetada como ƒH. La distancia entre estos dos puntos, es decir ( ƒH – ƒL ) se llama Ancho de banda, (BW) y es el rango de frecuencias sobre el cual se proporciona al menos la mitad de la potencia y corriente máximas como se muestra:

Ancho de banda de un circuito de resonancia en serie

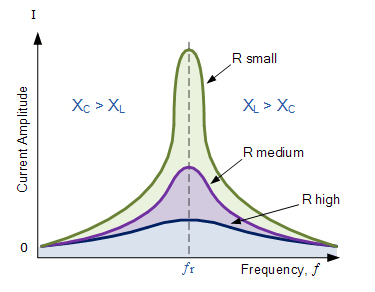
La respuesta de frecuencia de la magnitud actual de los circuitos anteriores se relaciona con la «nitidez» de la resonancia en un circuito de resonancia en serie. La nitidez del pico se mide cuantitativamente y se denomina factor de calidad, Q del circuito. El factor de calidad relaciona la energía máxima o pico almacenada en el circuito (la reactancia) con la energía disipada (la resistencia) durante cada ciclo de oscilación, lo que significa que es una relación entre la frecuencia resonante y el ancho de banda y cuanto mayor es el circuito Q, menor el ancho de banda, Q = ƒr / BW.

Como el ancho de banda se toma entre los dos puntos de -3dB, la selectividad del circuito es una medida de su capacidad para rechazar cualquier frecuencia a ambos lados de estos puntos. Un circuito más selectivo tendrá un ancho de banda más estrecho, mientras que un circuito menos selectivo tendrá un ancho de banda más amplio. La selectividad de un circuito de resonancia en serie se puede controlar mediante el ajuste del valor de la resistencia solamente, manteniendo todos los otros componentes de la misma, ya que Q = (XL o XC)/R.

Ancho de banda de un circuito de resonancia en serie RLC

Entonces, la relación entre resonancia, ancho de banda, selectividad y factor de calidad para un circuito de resonancia en serie se define como:

1). Frecuencia de resonancia, (ƒr)

2). Corriente, (I)

3). Frecuencia de corte más baja, (ƒL)

4). Frecuencia de corte superior, (ƒH)

5). Ancho de banda, (BW)

6). Factor de calidad, (Q)

Ejemplo de resonancia en serie No1

Una red de resonancia en serie que consta de una resistencia de 30Ω, un capacitor de 2uF y un inductor de 20mH se conecta a través de una tensión de alimentación sinusoidal que tiene una salida constante de 9 voltios en todas las frecuencias. Calcule la frecuencia de resonancia, la corriente en resonancia, el voltaje a través del inductor y el capacitor en resonancia, el factor de calidad y el ancho de banda del circuito. También dibuje la forma de onda de corriente correspondiente para todas las frecuencias.

1. Frecuencia de resonancia, ƒr

2. Corriente del circuito en la resonancia, Im

3. Reactancia inductiva en la resonancia, XL

4. Voltajes a través del inductor y el capacitor, VL, VC

Nota: la tensión de alimentación puede ser de solo 9 voltios , pero en resonancia, los voltajes reactivos a través del capacitor, VC y el inductor, VL son 30 voltios pico.

5. Factor de calidad, Q

6. Ancho de banda, BW

7. Los puntos de frecuencia superior e inferior de -3dB, ƒH y ƒL

8. Forma de onda de corriente

Ejemplo de resonancia en serie No2

Un circuito en serie consta de una resistencia de 4Ω, una inductancia de 500mH y una capacitancia variable conectada a través de una fuente de 100 V, 50 Hz. Calcule la capacitancia requerida para producir una condición de resonancia en serie y los voltajes generados tanto en el inductor como en el capacitor en el punto de resonancia.

Frecuencia de resonancia, ƒr

Voltajes a través del inductor y el capacitor, VL, VC

Resumen de resonancia en serie

Es posible que haya notado que durante el análisis de los circuitos de resonancia en serie en este tutorial, observamos el ancho de banda, las frecuencias superior e inferior, puntos de -3dB y calidad o factor Q. Todos estos son términos utilizados en el diseño y construcción de filtros de paso de banda (BPF) y, de hecho, los circuitos de resonancia se utilizan en diseños de filtros de red de 3 elementos para pasar todas las frecuencias dentro del rango de «banda de paso» y rechazar todas las demás.

Sin embargo, el objetivo principal de este tutorial es analizar y comprender el concepto de cómo se produce la resonancia en serie en los circuitos pasivos de la serie RLC. Su uso en redes y diseños de filtros RLC está fuera del alcance de este tutorial en particular, por lo que no se analizará aquí:

• Para que se produzca resonancia en cualquier circuito, debe tener al menos un inductor y un condensador.
• La resonancia es el resultado de las oscilaciones en un circuito cuando la energía almacenada pasa del inductor al condensador.
• La resonancia ocurre cuando XL = XC y la parte imaginaria de la función de transferencia es cero.
• En la resonancia de la impedancia del circuito es igual al valor de la resistencia como Z =R.
• A bajas frecuencias, el circuito en serie es capacitivo como: XC > XL, esto le da al circuito un factor de potencia líder.
• A altas frecuencias, el circuito en serie es inductivo como: XL > XC, esto le da al circuito un factor de potencia rezagado.
• El alto valor de corriente en resonancia produce valores muy altos de voltaje a través del inductor y el capacitor.
• Los circuitos de resonancia en serie son útiles para construir filtros selectivos de alta frecuencia. Sin embargo, su alta corriente y los valores muy altos de voltaje de los componentes pueden dañar el circuito.
• La característica más destacada de la respuesta de frecuencia de un circuito resonante es un pico resonante agudo en sus características de amplitud.
• Debido a que la impedancia es mínima y la corriente máxima, los circuitos de resonancia en serie también se denominan Circuitos Aceptadores.

En el próximo tutorial sobre resonancia en paralelo, veremos cómo la frecuencia afecta las características de un circuito RLC conectado en paralelo y cómo esta vez el factor Q de un circuito resonante en paralelo determina su aumento actual.