Triángulo de potencia y factor de potencia

Vimos en nuestro tutorial sobre energía eléctrica que los circuitos de CA que contienen resistencia y capacitancia o resistencia y la inductancia, o ambas, también contienen potencia real y potencia reactiva. Entonces, para que podamos calcular la potencia total consumida, necesitamos conocer la diferencia de fase entre las formas de onda sinusoidales del voltaje y la corriente.

En un circuito de CA, las formas de onda de voltaje y corriente son sinusoidales, por lo que sus amplitudes cambian constantemente con el tiempo. Como sabemos que la potencia es el voltaje multiplicado por la corriente (P = V * I), la potencia máxima se producirá cuando las dos formas de onda de voltaje y corriente se alineen entre sí. Es decir, sus picos y puntos de cruce cero ocurren al mismo tiempo. Cuando esto sucede, se dice que las dos formas de onda están «en fase».

Los tres componentes principales en un circuito de CA que pueden afectar la relación entre las formas de onda de voltaje y corriente, y por lo tanto su diferencia de fase, al definir la impedancia total del circuito, son la resistencia, el condensador y el inductor.

La impedancia, (Z) de un circuito de CA es equivalente a la resistencia calculada en circuitos de CC, con impedancia expresada en ohmios. Para los circuitos de CA, la impedancia se define generalmente como la relación entre el fasor de voltaje y corriente producidos por un componente del circuito. Los fasores son líneas rectas dibujadas de tal manera que representan un voltaje o amplitud de corriente por su longitud y su diferencia de fase con respecto a otras líneas fasoriales por su posición angular con respecto a los otros fasores.

Los circuitos de CA contienen resistencia y reactancia que se combinan para dar una impedancia total (Z) que limita el flujo de corriente alrededor del circuito. Pero la impedancia de un circuito de CA no es igual a la suma algebraica de los valores óhmicos resistivo y reactivo, ya que una resistencia pura y una reactancia pura están desfasadas 90° entre sí. Pero podemos usar esta diferencia de fase de 90° como los lados de un triángulo rectángulo, llamado triángulo de impedancia, siendo la impedancia la hipotenusa determinada por el teorema de Pitágoras.

Esta relación geométrica entre resistencia, reactancia e impedancia se puede representar visualmente mediante el uso de un triángulo de impedancia como se muestra:

Triángulo de impedancia

Tenga en cuenta que la impedancia, que es la suma vectorial de la resistencia y la reactancia, no solo tiene una magnitud (Z) sino que también tiene un ángulo de fase (Φ), que representa la diferencia de fase entre la resistencia y la reactancia. También tenga en cuenta que el triángulo cambiará de forma debido a variaciones en la reactancia, (X) a medida que cambia la frecuencia. Por supuesto, la resistencia (R) siempre permanecerá constante.

Podemos llevar esta idea un paso más allá al convertir el triángulo de impedancia en un triángulo de potencia que representa los tres elementos de potencia en un circuito de CA. La ley de Ohm nos dice que en un circuito de CC, la potencia (P), en vatios, es igual a la corriente al cuadrado (I2) por la resistencia (R). Entonces podemos multiplicar los tres lados de nuestro triángulo de impedancia anterior por I2 para obtener el triángulo de potencia correspondiente como:

Potencia real P = I2R Watts, (W)

Potencia reactiva Q = I2X Voltios-amperios reactiva, (VAr)

Potencia aparente S = I2Z Voltios-amperios, (VA)

Potencia real en circuitos de CA

La potencia real (P), también conocida como potencia real o activa, realiza el “trabajo real” dentro de un circuito eléctrico. La potencia real, medida en vatios, define la potencia consumida por la parte resistiva de un circuito. Entonces la potencia real, (P) en un circuito de CA es la misma que la potencia, P en un circuito de CC. Entonces, al igual que los circuitos de CC, siempre se calcula como I2* R, donde R es el componente resistivo total del circuito.

Como las resistencias no producen ninguna diferencia fasorial (cambio de fase) entre las formas de onda de voltaje y corriente, toda la potencia útil se entrega directamente a la resistencia y se convierte en calor, luz y trabajo. Entonces, la potencia consumida por una resistencia es la potencia real, que es fundamentalmente la potencia media de los circuitos.

Para encontrar el valor correspondiente de la potencia real, los valores rms de voltaje y corriente se multiplican por el coseno del ángulo de fase, Φ como se muestra:

Potencia real P = I2R = V * I * cos (Φ) Watts, (W)

Pero como no hay diferencia de fase entre el voltaje y la corriente en un circuito resistivo, el cambio de fase entre las dos formas de onda será cero (0). Entonces:

Potencia real en un circuito de CA

Donde la potencia real (P) está en vatios, el voltaje (V) está en voltios rms y la corriente (I) está en amperios rms.

Entonces, la potencia real es el I2* R del elemento resistivo medido en vatios, que es lo que lee en el medidor de energía de su servicio público y tiene unidades en vatios (W), kilovatios (kW) y megavatios (MW). Tenga en cuenta que la potencia real P, siempre es positiva.

Potencia reactiva en circuitos de CA

La potencia reactiva (Q), (a veces llamada potencia sin vatios) es la potencia consumida en un circuito de CA que no realiza ningún trabajo útil pero tiene un gran efecto en el cambio de fase entre las formas de onda de voltaje y corriente. La potencia reactiva está ligada a la reactancia producida por inductores y condensadores y contrarresta los efectos de la potencia real. La potencia reactiva no existe en los circuitos de CC.

A diferencia de la potencia real (P) que hace todo el trabajo, la potencia reactiva (Q) quita energía a un circuito debido a la creación y reducción de campos magnéticos inductivos y campos electrostáticos capacitivos, lo que dificulta que la potencia verdadera suministre energía directamente a un circuito o carga.

La energía almacenada por un inductor en su campo magnético intenta controlar la corriente, mientras que la energía almacenada por un campo electrostático de condensadores intenta controlar el voltaje. El resultado es que los condensadores «generan» potencia reactiva y los inductores «consumen» potencia reactiva. Esto significa que ambos consumen y devuelven energía a la fuente, por lo que no se consume nada de la energía real.

Para encontrar la potencia reactiva, los valores rms de voltaje y corriente se multiplican por el seno del ángulo de fase, Φ como se muestra:

Potencia reactiva Q = I2X = V * I * sin (Φ) voltios-amperios reactivos, (VAr)

Como hay una diferencia de fase de 90° entre las formas de onda de voltaje y corriente en una reactancia pura (inductiva o capacitiva), multiplicar V * I por sin (Φ) da una componente vertical que está 90° fuera de fase con cada otro, entonces:

Potencia reactiva en un circuito de CA

Donde la potencia reactiva (Q) está en voltios-amperios reactiva, el voltaje (V) está en voltios rms y la corriente (I) está en amperios rms.

Entonces la potencia reactiva representa el producto de voltios y amperios que están desfasados 90° entre sí, pero en general, puede haber cualquier ángulo de fase, Φ entre el voltaje y la corriente.

Por lo tanto, la potencia reactiva es el I2 *X del elemento reactivo que tiene unidades en voltios-amperios reactivos (VAr), kilovoltios-amperios reactivos (kVAr) y megavoltios-amperios reactivos (MVAr).

Potencia aparente en circuitos de CA

Hemos visto anteriormente que la potencia real se disipa por la resistencia y que la potencia reactiva se suministra a una reactancia. Como resultado de esto, las formas de onda de corriente y voltaje no están en fase debido a la diferencia entre los componentes resistivos y reactivos de un circuito.

Entonces hay una relación matemática entre la potencia real (P) y la potencia reactiva (Q), llamada potencia compleja. El producto del voltaje Vrms, aplicado a un circuito de CA y la corriente Irms, que fluye hacia ese circuito se llama «producto voltio-amperio» (VA) dado el símbolo S y cuya magnitud se conoce generalmente como potencia aparente.

Esta potencia compleja no es igual a la suma algebraica de las potencias real y reactiva sumadas, sino que es la suma vectorial de P y Q expresada en voltios-amperios (VA). Es una potencia compleja que está representada por el triángulo de potencia. El valor eficaz del producto voltio-amperio se conoce más comúnmente como potencia aparente, ya que «aparentemente» es la potencia total consumida por un circuito, aunque la potencia real que hace el trabajo es mucho menor.

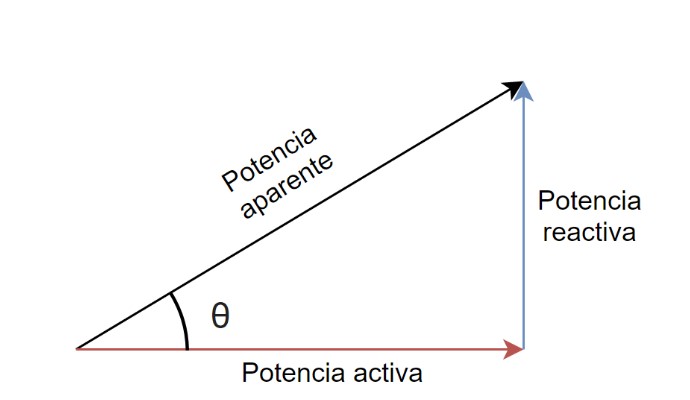
Como la potencia aparente se compone de dos partes, la potencia resistiva que es la potencia en fase o potencia real en vatios y la potencia reactiva que es la potencia fuera de fase en voltios-amperios, podemos mostrar la suma vectorial de estos dos componentes de potencia en forma de triángulo de potencia. Un triángulo de potencia tiene cuatro partes: P, Q, S y θ.

Los tres elementos que componen la energía en un circuito de CA se pueden representar gráficamente por los tres lados de un triángulo rectángulo, de la misma manera que el triángulo de impedancia anterior. El lado horizontal (adyacente) representa la potencia real del circuito (P), el lado vertical (opuesto) representa la potencia reactiva del circuito (Q) y la hipotenusa representa la potencia aparente resultante (S), del triángulo de potencia como se muestra:

Triángulo de potencia de un circuito de CA

• Donde:
• P es la I2* R o potencia real que realiza el trabajo medido en vatios, W
• Q es la I2* X o potencia reactiva medida en voltios-amperios reactiva, VAr
• S es la I2* Z o potencia aparente medida en voltios-amperios, VA
• Φ es el ángulo de fase en grados. Cuanto mayor sea el ángulo de fase, mayor será la potencia reactiva
• Cos (Φ) = P / S = W / VA = factor de potencia, pf
• Sin (Φ) = Q / S = VAr / VA
• Tan (Φ) = Q / P = VAr / W

El factor de potencia se calcula como la relación entre la potencia real y la potencia aparente porque esta relación es igual a cos (Φ).

Factor de potencia en circuitos de CA

El factor de potencia, cos (Φ), es una parte importante de un circuito de CA que también se puede expresar en términos de impedancia o potencia del circuito. El factor de potencia se define como la relación entre la potencia real (P) y la potencia aparente (S), y generalmente se expresa como un valor decimal, por ejemplo, 0,95, o como un porcentaje: 95%.

El factor de potencia define el ángulo de fase entre las formas de onda de corriente y voltaje, donde I y V son las magnitudes de los valores rms de la corriente y el voltaje. Tenga en cuenta que no importa si el ángulo de fase es la diferencia de la corriente con respecto al voltaje, o el voltaje con respecto a la corriente. La relación matemática se da como:

Factor de potencia de un circuito de CA

Anteriormente dijimos que en un circuito resistivo puro, las formas de onda de corriente y voltaje están en fase entre sí, por lo que la potencia real consumida es la misma que la potencia aparente, ya que la diferencia de fase es cero grados (0°). Entonces el factor de potencia será:

Factor de potencia, pf = cos 0°  = 1.0

Es decir, la cantidad de vatios consumidos es la misma que la cantidad de voltios-amperios consumidos, lo que produce un factor de potencia de 1.0 o 100%. En este caso, se refiere a un factor de potencia unitario.

También dijimos anteriormente que en un circuito puramente reactivo, las formas de onda de corriente y voltaje están desfasadas entre sí en 90°. Como la diferencia de fase es de noventa grados (90°), el factor de potencia será:

Factor de potencia, pf = cos 90°  = 0

Esa es la cantidad de vatios consumidos es cero, pero todavía hay un voltaje y una corriente que suministran la carga reactiva. Claramente, entonces la reducción del componente VAr reactivo del triángulo de potencia hará que θ se reduzca mejorando el factor de potencia hacia uno, la unidad. También es deseable tener un factor de potencia alto ya que esto hace el uso más eficiente del circuito que entrega corriente a una carga.

Entonces podemos escribir la relación entre la potencia real, la potencia aparente y el factor de potencia de los circuitos como:

Un circuito inductivo donde la corriente «retrasa» el voltaje (ELI) se dice que tiene un factor de potencia rezagado, y un circuito capacitivo donde la corriente «adelanta» el voltaje (ICE) se dice que tiene un factor de potencia adelantado.

Ejemplo de triángulo de potencia No1

Una bobina enrollada que tiene una inductancia de 180 mH y una resistencia de 35 Ω está conectada a una fuente de 100 V 50 Hz. Calcule: a) la impedancia de la bobina, b) la corriente, c) el factor de potencia y d) la potencia aparente consumida.

También dibuja el triángulo de potencia resultante para la bobina anterior.

Datos proporcionados: R = 35Ω, L = 180mH, V = 100V y ƒ = 50Hz.

(a) Impedancia (Z) de la bobina:

(b) Corriente (I) consumida por la bobina:

(c) El factor de potencia y el ángulo de fase, Φ:

(d) Potencia aparente (S) consumida por la bobina:

(e) Triángulo de potencia para la bobina:

Como demuestran las relaciones del triángulo de potencia de este ejemplo simple, con un factor de potencia de 0,5263 o 52,63%, la bobina requiere 150 VA de potencia para producir 79 vatios de trabajo útil. En otras palabras, con un factor de potencia del 52,63%, la bobina necesita aproximadamente un 89% más de corriente para hacer el mismo trabajo, que es una gran cantidad de corriente desperdiciada.

Agregar un capacitor de corrección del factor de potencia (para este ejemplo, 32.3uF) a través de la bobina, para aumentar el factor de potencia a más de 0.95, o 95%, reduciría en gran medida la potencia reactiva consumida por la bobina, ya que estos capacitores actúan como corriente reactiva. generadores, reduciendo así la cantidad total de corriente consumida.

Resumen del triángulo de potencia y factor de potencia 

Hemos visto aquí que los tres elementos de la energía eléctrica, potencia activa, potencia reactiva y aparente en un circuito de CA pueden ser representados por los tres lados de un triángulo llamado Triángulo de potencia. Como estos tres elementos están representados por un “triángulo rectángulo”, su relación se puede definir como: S2 = P2 + Q2, donde: P es la potencia real en vatios (W), Q es la potencia reactiva en voltios-amperios reactivos (VAr) y S es la potencia aparente en voltios-amperios (VA).

También hemos visto que en un circuito de CA, la cantidad cos (Φ) se llama factor de potencia. El factor de potencia de un circuito de CA se define como la relación entre la potencia real (W) consumida por un circuito y la potencia aparente (VA) consumida por el mismo circuito. Por lo tanto, esto nos da: Factor de potencia = potencia real / potencia aparente, o pf = W / VA.

Entonces, el coseno del ángulo resultante entre la corriente y el voltaje es el factor de potencia. Generalmente, el factor de potencia se expresa como un porcentaje, por ejemplo, 95%, pero también se puede expresar como un valor decimal, por ejemplo 0,95.

Cuando el factor de potencia es igual a 1.0 (unidad) o 100%, es decir, cuando la potencia real consumida es igual a la potencia aparente del circuito, el ángulo de fase entre la corriente y la tensión es 0° como: cos-1(1.0) = 0°. Cuando el factor de potencia es igual a cero (0), el ángulo de fase entre la corriente y la tensión será de 90° como: cos-1(0) = 90°. En este caso, la potencia real consumida por el circuito de CA es cero independientemente de la corriente del circuito.

En los circuitos de CA prácticos, el factor de potencia puede estar entre 0 y 1,0, dependiendo de los componentes pasivos dentro de la carga conectada. Para una carga o circuito inductivo-resistivo (que es el caso más frecuente), el factor de potencia estará “retrasado”. En un circuito capacitivo-resistivo, el factor de potencia será «adelantado». Entonces, un circuito de CA se puede definir para que tenga un factor de potencia unitario, rezagado o adelantado.

Un factor de potencia pobre con un valor cercano a cero (0) consumirá energía desperdiciada reduciendo la eficiencia del circuito, mientras que un circuito o carga con un factor de potencia más cercano a uno (1.0) o unidad (100%), será más eficiente. Esto se debe a que un circuito o carga con un factor de potencia bajo requiere más corriente que el mismo circuito o carga con un factor de potencia más cercano a 1.0 (unidad).