Inductancia mutua

En el tutorial anterior vimos que un inductor genera una fem inducida dentro de sí mismo como resultado del campo magnético cambiante alrededor del suyo. Cuando esta fem se induce en el mismo circuito en el que está cambiando la corriente, este efecto se denomina autoinducción, (L).

Sin embargo, cuando la fem se induce en una bobina adyacente situada dentro del mismo campo magnético, se dice que la fem se induce magnéticamente, inductivamente o por inducción mutua, símbolo (M). Luego, cuando dos o más bobinas están unidas magnéticamente por un flujo magnético común, se dice que tienen la propiedad de inductancia mutua.

La inductancia mutua es el principio de funcionamiento básico del transformador, motores, generadores y cualquier otro componente eléctrico que interactúe con otro campo magnético. Entonces podemos definir la inducción mutua como la corriente que fluye en una bobina que induce un voltaje en una bobina adyacente.

Pero la inductancia mutua también puede ser algo malo, ya que la inductancia “perdida” o de “fuga” de una bobina puede interferir con el funcionamiento de otro componente adyacente por medio de inducción electromagnética, por lo que puede ser necesaria alguna forma de apantallamiento eléctrico a un potencial de tierra.

La cantidad de inductancia mutua que une una bobina a otra depende en gran medida del posicionamiento relativo de las dos bobinas. Si una bobina se coloca al lado de la otra bobina de manera que su distancia física es pequeña, entonces casi todo el flujo magnético generado por la primera bobina interactuará con las vueltas de la bobina de la segunda bobina induciendo una fem relativamente grande y, por lo tanto, produciendo una gran valor de inductancia mutua.

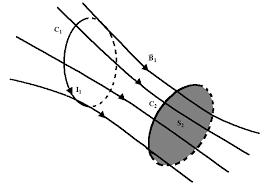
Del mismo modo, si las dos bobinas están más separadas entre sí o en ángulos diferentes, la cantidad de flujo magnético inducido desde la primera bobina a la segunda será más débil y producirá una fem inducida mucho menor y, por lo tanto, un valor de inductancia mutua mucho menor. Entonces, el efecto de la inductancia mutua depende en gran medida de las posiciones relativas o el espaciado (S) de las dos bobinas y esto se demuestra a continuación.

Inductancia mutua entre bobinas

La inductancia mutua que existe entre las dos bobinas se puede aumentar en gran medida colocándolas en un núcleo de hierro dulce común o aumentando el número de vueltas de cualquiera de las bobinas como se encontraría en un transformador.

Si las dos bobinas se enrollan firmemente una encima de la otra sobre un núcleo común de hierro dulce, se dice que existe un acoplamiento entre ellas, ya que cualquier pérdida debida a la fuga de flujo será extremadamente pequeña. Luego, suponiendo un enlace de flujo perfecto entre las dos bobinas, la inductancia mutua que existe entre ellas se puede dar como.

• Dónde:
•         µo es la permeabilidad del espacio libre (4.π.10-7)
•         µr es la permeabilidad relativa del núcleo de hierro dulce
•         N está en el número de vueltas de la bobina
•         A está en el área de la sección transversal en m2
•         ℓ es la longitud de las bobinas en metros

Inducción mutua

Aquí, la corriente que fluye en la bobina uno, L1 establece un campo magnético alrededor de sí mismo con algunas de estas líneas de campo magnético que pasan a través de la bobina dos, L2 nos da inductancia mutua. La bobina uno tiene una corriente de I1 y N1 vueltas, mientras que la bobina dos tiene N2 vueltas. Por lo tanto, la inductancia mutua, M12 de la bobina dos que existe con respecto a la bobina uno depende de su posición con respecto a la otra y se da como:

Del mismo modo, el flujo que une la bobina uno, L1 cuando una corriente fluye alrededor de la bobina dos, L2 es exactamente el mismo que el flujo que une la bobina dos cuando la misma corriente fluye alrededor de la bobina uno arriba, entonces la inductancia mutua de la bobina uno con respecto a la bobina dos se define como M21. Esta inductancia mutua es cierta independientemente del tamaño, número de vueltas, posición relativa u orientación de las dos bobinas. Debido a esto, se puede escribir la inductancia mutua entre las dos bobinas como: M12 = M21 =M.

Entonces podemos ver que la autoinductancia caracteriza a un inductor como un elemento de circuito único, mientras que la inductancia mutua significa alguna forma de acoplamiento magnético entre dos inductores o bobinas, dependiendo de su distancia y disposición, y con suerte recordamos de nuestros tutoriales sobre electroimanes que la autoinductancia de cada bobina individual se da como:

y

Al multiplicar de forma cruzada las dos ecuaciones anteriores, la inductancia mutua, M que existe entre las dos bobinas, se puede expresar en términos de la autoinductancia de cada bobina.

Dándonos una expresión final y más común para la inductancia mutua entre las dos bobinas de:

Inductancia mutua entre bobinas

Sin embargo, la ecuación anterior supone una fuga de flujo cero y un acoplamiento magnético del 100% entre las dos bobinas, L1 y L2. En realidad, siempre habrá alguna pérdida por fuga y posición, por lo que el acoplamiento magnético entre las dos bobinas nunca puede alcanzar o superar el 100%, pero puede acercarse mucho a este valor en algunas bobinas inductivas especiales.

Si parte del flujo magnético total se enlaza con las dos bobinas, esta cantidad de enlace de flujo se puede definir como una fracción del posible enlace de flujo total entre las bobinas. Este valor fraccionario se llama coeficiente de acoplamiento y se le da la letra k.

Coeficiente de acoplamiento

Generalmente, la cantidad de acoplamiento inductivo que existe entre las dos bobinas se expresa como un número fraccionario entre 0 y 1 en lugar de un valor porcentual (%), donde 0 indica cero o ningún acoplamiento inductivo, y 1 indica inductivo total o máximo acoplamiento.

En otras palabras, si k = 1 las dos bobinas están perfectamente acopladas, si k> 0,5 se dice que las dos bobinas están estrechamente acopladas y si k <0,5 las dos bobinas están débilmente acopladas. Entonces, la ecuación anterior, que supone un acoplamiento perfecto, se puede modificar para tener en cuenta este coeficiente de acoplamiento, k y se da como:

Factor de acoplamiento entre bobinas

O

Cuando el coeficiente de acoplamiento, k es igual a 1, (unidad) tal que todas las líneas de flujo de una bobina corta todas las espiras de la segunda bobina, es decir, las dos bobinas están estrechamente acopladas, la inductancia mutua resultante será ser igual a la media geométrica de las dos inductancias individuales de las bobinas.

Además, cuando las inductancias de las dos bobinas son iguales e iguales, L1 es igual a L2, la inductancia mutua que existe entre las dos bobinas será igual al valor de una sola bobina ya que la raíz cuadrada de dos valores iguales es la misma como un solo valor como se muestra.

Ejemplo de inductancia mutua No.1

Dos inductores cuyas autoinductancias se dan como 75 mH y 55 mH respectivamente, se colocan uno al lado del otro en un núcleo magnético común de modo que el 75% de las líneas de flujo de la primera bobina están cortando la segunda bobina. Calcule la inductancia mutua total que existe entre las dos bobinas.

Ejemplo de inductancia mutua  No. 2 

Cuando se enrollaron uniformemente dos bobinas que tenían inductancias de 5H y 4H respectivamente sobre un núcleo no magnético, se encontró que su inductancia mutua era de 1,5H. Calcule el coeficiente de acoplamiento que existe entre ellas.

En el siguiente tutorial sobre inductores, veremos cómo conectar inductores en serie y el efecto que tiene esta combinación en la inductancia mutua de los circuitos, la inductancia total y sus voltajes inducidos.