Inductancia de CA

Los inductores almacenan su energía en forma de un campo magnético que se crea cuando se aplica un voltaje a los terminales de un inductor. El crecimiento de la corriente que fluye a través del inductor no es instantáneo, sino que está determinado por el valor de fem inducido o inverso del inductor. Entonces, para un inductor este voltaje EMF trasero VL es proporcional a la tasa de cambio de la corriente que fluye a través de ella.

Esta corriente continúa aumentando hasta que alcanza su estado estable máximo, que es aproximadamente cinco constantes de tiempo cuando está fem de retorno autoinducida se ha reducido a cero. En este punto, una corriente de estado estable fluye a través de la bobina, la EMF de retorno ya no se induce para contrarrestar el flujo de corriente y, por lo tanto, la bobina actúa más como un cortocircuito que permite que la corriente máxima fluya a través de ella.

Sin embargo, en un circuito de CA que contiene un inductor CA, el flujo de corriente a través de un inductor se comporta de manera muy diferente al de un voltaje de CC constante. En un circuito de CA, la resistencia a la corriente que fluye a través de los devanados de la bobina depende no solo de la inductancia de la bobina, sino también de la frecuencia de la forma de onda de voltaje aplicada, ya que varía de sus valores positivos a negativos.

La resistencia real a la corriente que fluye a través de una bobina en un circuito de CA está determinada por la resistencia de CA de la bobina, cuya resistencia de CA está representada por un número complejo. Sin embargo, para distinguir un valor de resistencia de CC de un valor de resistencia de CA, que también se conoce como impedancia, el término reactancia se utiliza.

Al igual que la resistencia, la reactancia también se mide en ohmios, pero se le asigna el símbolo «X» para distinguirla de una puramente resistiva. Dado que el valor «R» del componente en cuestión es un inductor, la reactancia de un inductor se llama reactancia inductiva (XL) y se mide en ohmios. Su valor se puede tomar de la fórmula:

Reactancia inductiva

• Donde:
•    XL = reactancia inductiva en ohmios (Ω)
•    π (pi) = una constante numérica de 3,142
•    ƒ = frecuencia en Hertz (Hz)
•    L = inductancia en Henries, (H)

También podemos definir la reactancia inductiva en radianes, donde omega, ω es 2πƒ.

Entonces, cuando se aplica un voltaje sinusoidal a una bobina inductiva, el EMF trasero contrarresta el aumento y la caída de la corriente que fluye a través de la bobina, y en una bobina puramente inductiva que no tiene resistencia ni pérdidas, esa impedancia (el número complejo) es igual a su reactancia inductiva. La reactancia también está representada por un vector, ya que tiene un tamaño y una dirección (ángulo). Mira el circuito de abajo:

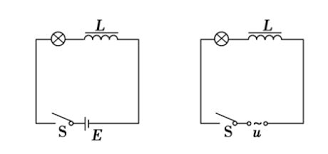
Inductancia CA con alimentación sinusoidal

Este circuito simple anterior consiste en una inductancia pura de L Henries (H) conectada a través de una tensión sinusoidal dada por la expresión: V (t) = Vmax sen ωt. Cuando el interruptor está cerrado, una corriente fluye a través de este voltaje sinusoidal y aumenta desde cero hasta su valor máximo. Este aumento o cambio en la corriente induce un campo magnético dentro de la bobina, que a su vez contrarresta o restringe este cambio en la corriente.

Sin embargo, antes de que la corriente tuviera tiempo de alcanzar su valor máximo, como en un circuito de CC, el voltaje cambia de polaridad, lo que hace que la corriente cambie de dirección. Este cambio en la otra dirección es retrasado nuevamente por el contador autoinducido EMK en la bobina, y en un circuito que solo contiene una inductancia pura, la corriente se retrasa 90°.

El voltaje aplicado alcanza su valor positivo máximo un cuarto (1 / 4ƒ) de ciclo antes de que la corriente alcance su valor máximo positivo, es decir, un voltaje aplicado a un circuito puramente inductivo «adelanta» la corriente en un cuarto de ciclo o 90° como se muestra a continuación:

Formas de onda sinusoidal para inductancia de CA

Este efecto también se puede representar mediante un diagrama fasorial en un circuito puramente inductivo, el voltaje «transporta» la corriente en 90°. Pero al usar el voltaje como nuestra referencia, también podemos decir que las «latencias» de corriente reducen el voltaje en un cuarto de ciclo o 90° como se muestra en el diagrama vectorial a continuación:

Diagrama vectorial para inductancia de corriente alterna.

Para un inductor puro de baja pérdida, VL IL «adelanta» en 90° o podemos decir que IL «se retrasa» VL en 90°.

Hay muchas formas diferentes de recordar la relación de fase entre el voltaje y la corriente que fluye a través de un circuito de inductancia pura. Sin embargo, un método muy simple y fácil de recordar es usar la expresión «ELI» (pronunciada como Ellie en el apellido de soltera). ELI significa Fuerza electromotriz primero en inductancia de corriente alterna, L antes de la corriente I. En otras palabras, el voltaje antes de la corriente en un inductor E, L, I es igual a «ELI», e independientemente del ángulo de fase en el que el comienza el voltaje, esta expresión siempre se aplica a un circuito de inductancia pura.

El efecto de la frecuencia sobre la reactancia inductiva

Cuando se conecta un suministro de 50 Hz a través de una inductancia de CA adecuada, la corriente se retrasa 90° como se describió anteriormente y se obtiene un valor máximo de I al final de cada mitad antes de que el voltaje invierta el ciclo de amperios de polaridad , es decir, la corriente aumenta «hasta su valor máximo T segundos».

Ahora, si aplicamos un suministro de 100 Hz a la bobina al mismo voltaje pico, la corriente aún se retrasará 90° pero su valor máximo será menor que el valor de 50 Hz como el tiempo que toma llegar a su valor máximo para lograr , se debe al aumento de frecuencia, porque ahora solo tiene «1/2 T segundos» para alcanzar su valor máximo. La tasa de cambio del flujo dentro de la bobina también ha aumentado debido al aumento de frecuencia.

A partir de la ecuación anterior para la reactancia inductiva, se puede ver que si la frecuencia o la inductancia aumenta, el valor de reactancia inductiva total de la bobina también aumentaría. Cuando la frecuencia aumenta y se acerca al infinito, la reactancia de los inductores y, por lo tanto, su impedancia también aumentaría hacia el infinito y actuaría como un circuito abierto.

A medida que la frecuencia se acerca a cero o CC, la reactancia de los inductores también disminuiría a cero y actuaría como un cortocircuito. Esto significa entonces que la reactancia inductiva es «directamente proporcional a la frecuencia» y tiene un valor pequeño a bajas frecuencias y un valor alto a frecuencias más altas, como se muestra:

Reactancia inductiva versus frecuencia

La reactancia inductiva de un inductor aumenta con el aumento de la frecuencia, por lo tanto, la reactancia inductiva es proporcional a la frecuencia ( XL α ƒ ) ya que la EMF trasera generada en el inductor es igual a su inductancia multiplicada por la tasa de cambio de la corriente en la inductancia.

A medida que aumenta la frecuencia, el valor de la corriente que fluye a través del inductor también disminuye.

Podemos representar el efecto de frecuencias muy bajas y muy altas sobre la reactancia de una inductancia de CA pura de la siguiente manera:

En un circuito de CA con inductancia pura, se aplica la siguiente fórmula:

¿Cómo obtuvimos esta ecuación? Bueno, la fem autoinducida en el inductor está determinada por la ley de Faraday, que crea el efecto de «autoinducción». Cuando una corriente fluye a través de una bobina inductiva, la tasa de cambio en la corriente alterna induce una fem en la misma bobina que contrarresta la corriente cambiante. El efecto sobre la bobina, en el que su propio campo magnético, generado por la corriente que la atraviesa, contrarresta un cambio de corriente, se conoce como «autoinductancia».

El valor de voltaje máximo de esta fem autoinducida corresponde a la tasa máxima de cambio de la corriente, donde este valor de voltaje a través de la bobina se da de la siguiente manera:

Donde: d / dt representa la tasa de cambio de la corriente con respecto al tiempo.

La corriente sinusoidal que fluye a través de la bobina de inducción (L) y crea el flujo magnético a su alrededor se da como:

Entonces, la ecuación anterior se puede reescribir de la siguiente manera:

La diferenciación de la corriente sinusoidal da como resultado:

La identidad trigonométrica de cos (ωt + 0o) = sin (ωt + 0 forma de onda del coseno 0 + 90+ 90o) como es efectivamente una forma de onda sinusoidal desplazada. Luego, podemos usar la ecuación anterior en forma de onda sinusoidal para definir el voltaje a través de una CA de la siguiente manera:

Donde: VMAX = ωLIMAX = √2VRMS, que es la máxima de voltaje, y θ = + 90° es el diferencia de fase o el ángulo de fase entre las formas de onda de voltaje y corriente. Es decir, la corriente está 90° por detrás del voltaje a través de un inductor puro.

En el dominio de fasor

El voltaje a través de la bobina se da de la siguiente manera:

y en forma polar esto se escribiría así: XL< 90° donde:

CA a través de un circuito en serie R + L

Hemos visto anteriormente que la corriente fluye a través de una bobina puramente inductiva que divide el voltaje entre 90° y cuando decimos una bobina puramente inductiva nos referimos a una que no tiene resistencia óhmica y, por lo tanto, no tiene pérdidas de I2R . En el mundo real, sin embargo, es imposible tener solo un inductor puro CA .

Todas las bobinas, relés, imanes y transformadores eléctricos tienen una cierta resistencia, independientemente de lo pequeñas que sean las espiras de bobina utilizadas. Esto se debe a que el alambre de cobre tiene una resistencia específica. Entonces podemos pensar en nuestra bobina de inducción como una bobina que tiene una resistencia, R en serie con una inductancia, con L creando lo que se conoce como una «inductancia impura».

Si la bobina tiene una resistencia «interna», necesitamos representar la impedancia total de la bobina como una resistencia en serie con un inductor y en un circuito de CA que contiene tanto la inductancia L como la resistencia R, siendo el voltaje V a través de la combinación la suma vectorial de los dos componentes de los voltajes VR y VL.

Esto significa entonces que la corriente que fluye a través de la bobina todavía está por detrás del voltaje, pero en una cantidad de menos de 90°, dependiendo de los valores de VR y VL, la suma vectorial. El nuevo ángulo entre las formas de onda de voltaje y corriente nos da su diferencia de fase, que se sabe que es el ángulo de fase del circuito con el símbolo griego phi, Φ.

Piensa en el siguiente circuito como una resistencia puramente, R está conectado en serie con un circuito  de serie L.

Serie de circuito resistencia- inductiva

En el circuito en serie RL anterior, podemos ver que la corriente tanto en la resistencia como en la inductancia juntas, mientras que el voltaje de los dos componentes voltajes VR y VL está compuesto. El voltaje resultante de estos dos componentes se puede determinar matemáticamente o dibujando un diagrama vectorial. Para generar el diagrama vectorial, se debe encontrar una referencia o componente común, y en un circuito de CA en serie, la corriente es la fuente de referencia porque la misma corriente fluye a través del resistor y el inductor. Los diagramas vectoriales individuales para una resistencia pura y una inductancia pura se muestran a continuación:

Diagramas vector para los dos componentes puros 

Podemos ver desde arriba y en nuestro tutorial anterior sobre la resistencia de CA que el voltaje y la corriente en un circuito de resistencia están en fase y, por lo tanto, el vector VR se superpone para escalar al vector actual. También se sabe desde arriba que la corriente se retrasa con respecto al voltaje en un circuito de inductancia de CA (puro), por lo tanto, el vector VL se dibuja 90° por delante de la corriente y en la misma escala que VR, como se muestra:

Diagrama vectorial del voltaje resultante.

En el diagrama vectorial anterior, podemos ver que la línea OB es la referencia de corriente horizontal y la línea OA es el voltaje a través del componente de resistencia que está en fase con la corriente. La línea OC muestra el voltaje inductivo, que está 90° por delante de la corriente, por lo que todavía se puede ver que la corriente de 90 voltios puramente inductivos se retrasa. La línea OD nos da la tensión de alimentación resultante, Entonces:

• V corresponde al valor rms del voltaje aplicado.
•  I  corresponde al valor rms de la corriente en serie.
• VR corresponde a la IR a caída de voltaje a través de la resistencia que está en fase con la corriente.
• VL corresponde a la IXL a caída de voltaje a través de la inductancia, que adelanta la corriente en 90°.

Si la corriente coloca el voltaje en una inductancia pura exactamente fasorial 90°, el diagrama resultante extraído de las caídas de voltaje individuales VR y VL representa un voltaje de triángulo rectángulo como se muestra arriba. OAD Entonces también podemos usar el teorema de Pitágoras para encontrar matemáticamente el valor de este voltaje resultante a través del circuito de resistencia / inductancia (RL).

Dado que VR = IR y VL = IXL, el voltaje aplicado es la suma vectorial de los dos de la siguiente manera:

representa la impedancia Z del circuito.

La impedancia de una CA inductante

La impedancia, Z es la resistencia «TOTAL» a la corriente que fluye en un circuito de CA, que contiene tanto la resistencia (la parte real) como la reactancia (la parte imaginaria). La impedancia también tiene las unidades de ohmios, Ω. La impedancia depende de la frecuencia ω del circuito, ya que esta influye en los componentes reactivos del circuito y todas las resistencias e impedancias reactivas se suman en una conexión en serie.

La impedancia también se puede representar mediante un número complejo, Z = R + jXL , pero no es un puntero, sino el resultado de dos o más punteros que se combinan entre sí. Si dividimos los lados del triángulo de voltaje I anterior, obtenemos otro triángulo, cuyos lados representan la resistencia, reactancia e impedancia del circuito como se muestra a continuación:

El triángulo de impedancia RL

Entonces:    (impedancia)2 = (resistencia)2 + ( j reactancia)2,  donde j representa el 90° del cambio de fase.

Esto significa que el ángulo de fase positivo θ entre el voltaje y la corriente se da como:

Ángulo de fase

Si bien nuestro ejemplo anterior representa una inductancia de CA no pura simple, la resistencia total para los elementos resistivos sería la misma si dos o más bobinas de inducción están conectadas en serie o una sola bobina está conectada en serie con muchas resistencias no inductivas hasta : R1 + R2 + R3 etc. lo que da una resistencia total para el circuito.

Así mismo, la reactancia total de los elementos inductivos sería la misma: X1 + X2 + X3 , etc., dando un valor de reactancia total para el circuito. De esta manera, un circuito que contiene muchas bobinas, bobinas y resistencias se puede reducir fácilmente a un valor de impedancia Z que consiste en una sola resistencia en serie con una sola reactancia Z2 = R2 + X2.

Ejemplo No. 1 para inductancia en CA

En el siguiente circuito, la tensión de alimentación se define de la siguiente manera: V(t) inductancia= 325 sen (314t – 30o ) y L = 2.2H. Determine el valor de la corriente rms que fluye a través de la bobina y dibuje el diagrama vectorial resultante.

La tensión efectiva en la bobina corresponde a la tensión de alimentación. Si el voltaje pico de la fuente de alimentación es 325 V, el valor eficaz equivalente es 230 V. La conversión de este valor en el dominio del tiempo a su forma polar da: VL = 230 ∠-30o (voltios). La reactancia inductiva de la bobina es: XL = ωL = 314 x 2.2 = 690Ω. Luego, la corriente que fluye a través de la bobina se puede determinar usando la ley de Ohm de la siguiente manera:

Con la corriente alrededor de 90° será el retraso del diagrama fasorial.

Ejemplo No. 2 para inductancia en CA

Una bobina tiene una resistencia de 30 Ω y una inductancia de 0.5 H. Si la corriente que fluye a través de la bobina es de 4 amperios. ¿Cuál es el valor eficaz de la tensión de alimentación cuando su frecuencia es de 50 Hz?

La impedancia del circuito es:

Luego, la caída de voltaje en cada componente se calcula de la siguiente manera:

El ángulo de fase entre la corriente y la tensión de alimentación se calcula como:

El diagrama fasorial será:

En el siguiente tutorial sobre capacitancia de CA, examinaremos la relación voltaje-corriente de un capacitor cuando se le aplica una forma de onda sinusoidal de CA de estado estable junto con su representación de diagrama fasorial para capacitores puros y no puros.