Filtro de variable de estado

Los filtros de variable de estado utilizan tres (o más) circuitos amplificadores operacionales (el elemento activo) conectados en cascada para producir las salidas de filtro individuales, pero si es necesario, también se puede agregar un amplificador sumador adicional para producir un cuarto filtro de muesca en respuesta de salida.

Los filtros de variable de estado son filtros activos RC de segundo orden que constan de dos integradores de amplificador operacional idénticos, cada uno de los cuales actúa como un filtro de paso bajo unipolar de primer orden, un amplificador sumador alrededor del cual podemos establecer la ganancia de los filtros y su retroalimentación de amortiguación la red. Las señales de salida de las tres etapas del amplificador operacional se retroalimentan a la entrada, lo que nos permite definir el estado del circuito.

Una de las principales ventajas de un diseño de filtro de variable de estado es que los tres parámetros principales de los filtros, ganancia (A), frecuencia de esquina, ƒC y los filtros Q se pueden ajustar o configurar de forma independiente sin afectar el rendimiento de los filtros.

De hecho, si se diseña correctamente, la frecuencia de esquina de -3dB,( ƒc punto) tanto para la respuesta de amplitud de paso bajo como para la respuesta de amplitud de paso alto, debe ser idéntica al punto de frecuencia central de la etapa de paso de banda. Es decir, ƒLP (-3dB) es igual a ƒHP (-3dB) que es igual a ƒBP (centro). Además, el factor de amortiguación, ( ζ ) para la respuesta del filtro de paso de banda debe ser igual a 1 / Q, ya que Q se establecerá en -3dB, (0,7071).

Aunque el filtro proporciona salidas de paso bajo (LP), paso alto (HP) y paso de banda (BP), la aplicación principal de este tipo de circuito de filtro es un diseño de filtro de paso de banda variable de estado con la frecuencia central establecida por los dos enteros RC .

Si bien hemos visto antes que las características de un filtro de paso de banda se pueden obtener simplemente conectando en cascada un filtro de paso bajo con un filtro de paso alto, los filtros de paso de banda variable de estado tienen la ventaja de que se pueden sintonizar para ofrecer una oferta altamente selectiva (alta Q) altas ganancias en el punto de frecuencia central.

Hay varios diseños de filtros de variable de estado disponibles, todos basados ​​en el diseño de filtro estándar, con variaciones disponibles tanto con inversión como sin inversión. Sin embargo, el diseño de filtro básico será el mismo para ambas variaciones, como se muestra en la siguiente representación del diagrama de bloques.

Diagrama de bloque de filtro de variable de estado

Luego, podemos ver en el diagrama de bloques básico anterior que el filtro de variable de estado tiene tres salidas posibles, VHP, VBP y VLP con una de cada uno de los tres amplificadores operacionales. También se puede lograr una respuesta de filtro de muesca mediante la adición de un cuarto amplificador operacional.

Con un voltaje de entrada constante, VIN la salida del amplificador sumador produce una respuesta de paso alto que también se convierte en la entrada del primer Integrador RC. La salida de este integrador produce una respuesta de paso de banda que se convierte en la entrada del segundo Integrador RC produciendo una respuesta de paso bajo en su salida. Como resultado, se pueden encontrar funciones de transferencia separadas para cada salida individual con respecto al voltaje de entrada.

Por lo tanto, el diseño básico de filtro de variable de estado no inversor se da como:

Circuito de filtro de variable de estado

y la respuesta de amplitud de las tres salidas del filtro de variable de estado se verá así:

Respuesta normalizada de un filtro de variable de estado

Uno de los principales elementos de diseño de un filtro de variable de estado es el uso de dos integradores de amplificador operacional. Como vimos en el tutorial de Integrador, los integradores de amplificadores operacionales utilizan una impedancia dependiente de la frecuencia en forma de condensador dentro de su circuito de retroalimentación. Cuando se usa un capacitor, el voltaje de salida es proporcional a la integral del voltaje de entrada como se muestra:

Circuito integrador de amplificador operacional

Para simplificar un poco las matemáticas, esto también se puede reescribir en el dominio de la frecuencia como:

El voltaje de salida Vout es una constante 1 / RC multiplicada por la integral del voltaje de entrada Vin con respecto al tiempo. Los integradores producen un retraso de fase con el signo menos ( – ) que indica un cambio de 180° de fase porque la señal de entrada está conectada directamente al terminal de entrada inversora del amplificador operacional.

En el caso del amplificador operacional A2 anterior, su señal de entrada está conectada a la salida del amplificador operacional en curso A1 por lo que su entrada se da como VHP y su salida como VBP. Luego, desde arriba, la expresión para amplificador operacional, A2 se puede escribir como:

Luego, reordenando esta fórmula, podemos encontrar la función de transferencia del integrador inversor, A2

Función de transferencia Op-amp A2 

Se puede hacer exactamente la misma suposición que la anterior para encontrar la función de transferencia para el otro integrador de amplificador operacional, A3

Función de transferencia Op-amp A3 

Entonces, los dos integradores de amplificador operacional, A2 y A3, están conectados en cascada, por lo que la salida del primero (VBP) se convierte en la entrada del segundo. Entonces podemos ver que la respuesta de paso de banda se crea integrando la respuesta de paso alto y la respuesta de paso bajo se crea integrando la respuesta de paso de banda. Por lo tanto, la función de transferencia entre VHP y VLP se da como:

Tenga en cuenta que cada etapa del integrador proporciona una salida invertida, pero la salida sumada será positiva ya que son integradores inversores. Sí exactamente los mismos valores para R y C, se utilizan de manera que los dos circuitos tienen la misma constante de tiempo del integrador, los dos circuitos amplificadores pueden ser considerados con un circuito integrador único que tenga una frecuencia de esquina, ƒC.

Además de los dos circuitos integradores, el filtro también tiene un amplificador sumador diferencial que proporciona una suma ponderada de sus entradas. La ventaja aquí es que las entradas al amplificador sumador, A1 combinan retroalimentación oscilatoria, amortiguación y señales de entrada al filtro, ya que las tres salidas se retroalimentan a las entradas sumadoras.

Circuito sumador del amplificador

El amplificador operacional, A1 está conectado como un circuito sumador-restador. Es decir, suma la señal de entrada, VIN con la salida VBP del amplificador operacional A2 y le resta la salida VLP del amplificador operacional A3, así:

y

Como las entradas diferenciales, + V y -V de un amplificador operacional son las mismas, es decir: + V – -V, podemos reorganizar las dos expresiones anteriores para encontrar la función de transferencia para la salida de A1, la salida de paso alto.

Sabemos por lo anterior, que VBP y VLP son las salidas de los dos integradores, A2 y A3 respectivamente. Sustituyendo las ecuaciones integradoras de A2 y A3 en la ecuación anterior, obtenemos que la función de transferencia del filtro de variable de estado sea:

Función de transferencia de filtro de variable de estado

Hemos dicho anteriormente que un filtro variable estado produce tres respuestas de filtro, de paso bajo, paso alto y de paso de banda y que la respuesta de paso de banda es la de un filtro muy estrecho alta Q y esto es evidente en la función de transferencia del SVF anterior, ya que se asemeja a la de una respuesta estándar de segundo orden.

Función de transferencia normalizada de segundo orden

La frecuencia de la esquina de los filtros, ƒC

Si hacemos que las resistencias de entrada de los integradores y los capacitores de retroalimentación sean iguales, entonces la frecuencia de la esquina de los filtros de variable de estado se puede sintonizar fácilmente sin afectar su general Q. Asimismo, el valor de Q se puede variar sin alterar la frecuencia de esquina. Entonces, la frecuencia de la esquina se da como:

Frecuencia de la esquina del filtro variable de estado

Si hacemos que las resistencias de retroalimentación tengan R3 y R4 los mismos valores, entonces la frecuencia de esquina de cada salida de filtro del filtro de variable de estado simplemente se convierte en:

Luego de la sintonización de la frecuencia de corte variable de estado se lleva a cabo simplemente variando ya sea la resistencia de sintonización, R o el condensador, C.

Los filtros de variables de estado se caracterizan no solo por sus respuestas de salida individuales, sino también por los filtros “Q”, el  factor de calidad se relaciona con la «nitidez» de la curva de respuesta de amplitud de los filtros de paso de banda y cuanto mayor es la Q, mayor o más nítida es la respuesta de salida, lo que da como resultado un filtro que es altamente selectivo.

Para un filtro de paso de banda, Q se define como la frecuencia central dividida por el ancho de banda de los filtros -3dB, es decir, Q = ƒc / BW. Pero Q también se puede encontrar a partir del denominador de la función de transferencia anterior, ya que es el recíproco del factor de amortiguación ( ζ ). Entonces Q se da como:

El factor Q de un filtro de variable de estado

Nuevamente, si las resistencias R3 y R4 son iguales y ambos componentes integradores R y C son iguales, entonces la expresión de raíz cuadrada final se reduciría a: √1 o simplemente 1 ya que el numerador y el denominador se cancelan entre sí.

Ejemplo de filtro de variable de estado No.1

Diseñe un filtro de variable de estado que tenga una frecuencia de esquina (natural no amortiguada), ƒC de 1 kHz y un factor de calidad, Q de 10. Suponga que tanto los resistores y los condensadores que determinan la frecuencia son iguales. Determine la ganancia de CC de los filtros y dibuje el circuito resultante y el diagrama de Bode.

Dijimos anteriormente que si tanto la resistencia, R como el capacitor de retroalimentación, C de los dos circuitos integradores tienen los mismos valores, es decir, R = R y C = C, el punto de frecuencia de corte o esquina para el filtro se da simplemente como:

Frecuencia de la esquina del filtro

Podemos elegir un valor para el resistor o el capacitor para encontrar el valor del otro. Si asumimos un valor adecuado de 10nF para el capacitor, entonces el valor de la resistencia será:

Dando C = 10nF y R = 15.9kΩ, o 16kΩ al valor preferido más cercano.

El valor de Q se da como 10. Esto se relaciona con el coeficiente de amortiguación de los filtros como:

En la función de transferencia de la variable de estado anterior, la parte 2ζ se reemplaza por la combinación de resistencias dando:

Sabemos desde arriba que R = 16kΩ y C = 10nF, pero si asumimos que las dos resistencias de retroalimentación , R3 y R4 son iguales e iguales a 10kΩ, entonces la ecuación anterior se reduce a:

Suponiendo un valor adecuado para la resistencia de entrada, R1 de digamos 1kΩ, entonces podemos encontrar el valor de R2 de la siguiente manera:

De la función de transferencia normalizada arriba, la ganancia de banda de paso de CC se define como A° y de la función de transferencia de filtro variable de estado equivalente esto equivale a:

Los filtros SVF Ganancia de banda de paso de CC.

Por lo tanto, la ganancia de voltaje de CC del filtro se calcula en 1.9, que básicamente equivale a R2 / R3. Además, la ganancia máxima del filtro en ƒC se puede calcular como: Ao x Q de la siguiente manera.

Filtros de máxima ganancia de SVF

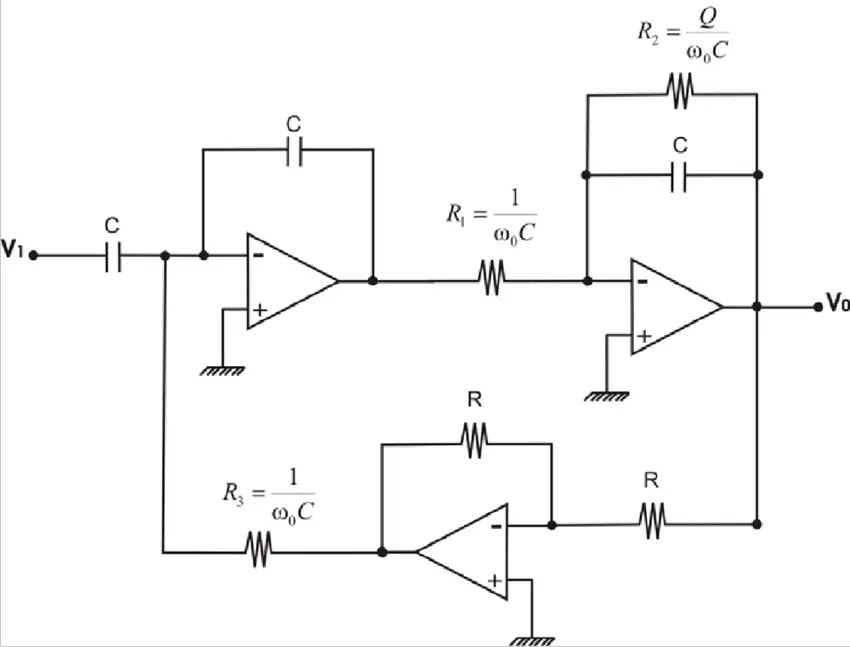
Circuito de filtro de variable de estado

A continuación, el diseño del circuito de filtro variable de estado será: R =16kΩ, C =10nF, R1 =1k, R2 = 19kΩ y R3 = R4 = 10 k como se muestra:

Diseño de filtro de variable de estado

Ahora podemos trazar las curvas de respuesta de salida individual para el circuito de filtro de variable de estado en un rango de frecuencias de 1Hz a 1MHz en un diagrama de Bode como se muestra:

Gráfico de Bode del filtro de variable de estado

Luego, podemos ver en las curvas de respuesta de los filtros anteriores, que la ganancia de CC del circuito del filtro es de 5.57dB, lo que equivale a una ganancia de voltaje de bucle abierto, Ao o 1.9 como se calculó anteriormente. La respuesta también muestra que las curvas de salida picos a una ganancia de voltaje máximo de 25.6dB en la frecuencia de corte debido al valor de Q. Como Q también relaciona la frecuencia central de los filtros de paso de banda con su ancho de banda, el ancho de banda del filtro será por lo tanto: ƒo/ 10 = 100Hz.

Hemos visto en este tutorial de filtro de variable de estado que en lugar de un filtro activo que produce un tipo de respuesta de frecuencia, podemos usar técnicas de retroalimentación múltiple para producir las tres respuestas de filtro, paso bajo, paso alto y paso de banda simultáneamente desde el mismo único activo diseño de filtros.

Pero además de las tres respuestas de filtro básicas, podemos agregar un circuito de amplificador operacional adicional al diseño de filtro de variable de estado básico anterior para producir una cuarta respuesta de salida similar a la de un filtro estándar de muesca.

Diseño de un filtro de muesca 

Es básicamente lo opuesto a un filtro de paso de banda, ya que rechaza o detiene una banda específica de frecuencias. Entonces, un filtro de muesca también se conoce como «filtro de parada de banda». Para obtener la respuesta de un filtro de muesca a partir del diseño de filtro de variable de estado básico, tenemos que sumar las respuestas de salida de paso alto y paso bajo utilizando otro amplificador sumador de amplificador operacional, A4 como se muestra:

Circuito de filtro de muesca

Aquí, para simplificar las cosas, hemos asumido que las dos resistencias de entrada, R5 y R6 , así como la resistencia de retroalimentación, R7 tienen el mismo valor de 10kΩ, al igual que para R3 y R4. Por lo tanto, esto le da al filtro de muesca una ganancia de 1, unidad.

La respuesta de salida del filtro de muesca y el filtro de paso de banda están relacionadas con la frecuencia central de la respuesta de paso de banda que es igual al punto de respuesta cero del filtro de muesca, y en este ejemplo será de 1 kHz.

Además, el ancho de banda de la muesca está determinado por los circuitos Q, exactamente igual que para la respuesta de banda de paso. Por lo tanto, el pico descendente es igual a la frecuencia central dividida por el ancho de banda de -3dB, que es la diferencia de frecuencia entre los puntos de -3dB a cada lado de la muesca. Tenga en cuenta que el factor de calidad Q no tiene nada que ver con la profundidad real de la muesca.

Este diseño de filtro de muesca básico (parada de banda) tiene solo dos entradas aplicadas a su amplificador sumador, la salida de paso bajo, VLP y la salida de paso alto, VHP. Sin embargo, hay dos señales más disponibles para usar desde el circuito de filtro variable de estado básico, la salida de paso de banda, VBP y la señal de entrada en sí, VIN.

Si una de estas dos señales también se utiliza como entrada al amplificador sumador del filtro de muesca junto con las señales de paso bajo y paso alto, entonces se puede controlar la profundidad de la muesca.

Dependiendo de cómo desee controlar la salida de la sección de filtro de muesca, dependerá de cuál de las dos señales disponibles usaría. Si fuera necesario que la muesca de salida cambie de una respuesta negativa a una respuesta positiva en la frecuencia natural no amortiguada ƒo, entonces la señal de salida de paso de banda VBP se utilizaría.

Asimismo, si se requiriera que la muesca de salida solo varíe en su profundidad negativa hacia abajo, entonces la señal de entrada, VIN se usaría. Si cualquiera de estas dos señales adicionales estuviera conectada al amplificador sumador del amplificador operacional a través de una resistencia variable, entonces la profundidad y la dirección de la muesca podrían controlarse por completo. Considere el circuito de filtro de muesca modificado a continuación:

Filtro de muesca de variable profunda

Resumen filtro de variable de estado

El filtro de variable de estado (SVF) es un diseño de filtro RC activo de segundo orden que utiliza múltiples técnicas de retroalimentación para producir tres salidas de respuesta de frecuencia diferentes, a saber: paso bajo, paso alto y paso de banda del mismo filtro único. La ventaja del filtro de variable de estado sobre otros diseños de filtro básico es que los tres parámetros principales del filtro, Gain, Q y ƒc se pueden ajustar de forma independiente.

También hemos visto aquí que el filtro también es fácil de sintonizar ya que la frecuencia de esquina, ƒc se puede configurar y ajustar variando R o C sin afectar el factor de amortiguación de los filtros. Sin embargo, a frecuencias de esquina más altas y factores de amortiguación más grandes, el filtro puede volverse inestable, por lo que es mejor usarlo con un bajo Q, menos de 10 y con frecuencias de esquina bajas.

El diseño de filtro de variable de estado básico utiliza tres secciones de amplificador operacional para producir sus salidas, pero también hemos visto que con la adición de una cuarta sección de amplificador operacional que suma las secciones de paso bajo y paso alto juntas, una muesca (parada de banda) La respuesta de salida del filtro también se puede lograr en la frecuencia central deseada.