Filtros de segundo orden

Los filtros de segundo orden que también se conocen como filtros VCVS, porque se utiliza el amplificador operacional como amplificador de fuente de voltaje controlado por voltaje, son otro tipo importante de diseño de filtro activo porque, junto con los filtros RC activos de primer orden que vimos anteriormente, se pueden diseñar circuitos de filtro de orden superior usándolos.

En los tutoriales de esta sección de filtros analógicos, hemos analizado los diseños de filtros pasivos y activos y hemos visto que los filtros de primer orden se pueden convertir fácilmente en filtros de segundo orden simplemente usando una red adicional RC dentro de la ruta de entrada o retroalimentación. Entonces podemos definir los filtros de segundo orden simplemente como: «dos filtros de primer orden en cascada junto con la amplificación».

La mayoría de los diseños de filtros de segundo orden generalmente llevan el nombre de su inventor, siendo los tipos de filtro más comunes: Butterworth, Chebyshev, Bessel y Sallen-Key. Todos estos tipos de diseños de filtros están disponibles como: filtro de paso bajo, filtro de paso alto, filtro de paso de banda y configuraciones de filtro de parada de banda (muesca), y al ser filtros de segundo orden, todos tienen una reducción de 40 dB por década.

El diseño del filtro Sallen-Key es uno de los diseños de filtro de segundo orden más conocidos y populares, que requiere solo un amplificador operacional único para el control de ganancia y cuatro componentes RC pasivos para realizar la sintonización.

La mayoría de los filtros activos constan solo de amplificadores operacionales, resistencias y capacitores, y el punto de corte se logra mediante el uso de retroalimentación, lo que elimina la necesidad de inductores como se usa en los circuitos de filtro pasivos de primer orden.

Los filtros activos de segundo orden (dos polos), ya sean de paso bajo o de paso alto, son importantes en electrónica porque podemos usarlos para diseñar filtros de orden mucho más alto con reducciones muy pronunciadas y al conectar en cascada filtros de primer y segundo orden, filtros analógicos con un n-ésimo valor de la orden, ya sea par o impar se pueden construir hasta cualquier valor, dentro de lo razonable.

Filtro de paso bajo de segundo orden 

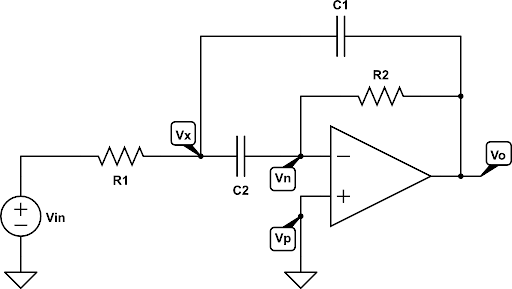
Los filtros de paso bajo de segundo orden son fáciles de diseñar y se utilizan ampliamente en muchas aplicaciones. La configuración básica para un filtro de paso bajo de segundo orden (dos polos) de Sallen-Key se da como:

Filtro de paso bajo de segundo orden

Este circuito de filtro de paso bajo de segundo orden tiene dos redes RC, R1 – C1 y R2 – C2 que le dan al filtro sus propiedades de respuesta de frecuencia. El diseño del filtro se basa en una configuración de amplificador operacional no inversor, por lo que la ganancia de los filtros, siempre será mayor que 1. Además, el amplificador operacional tiene una alta impedancia de entrada, lo que significa que se puede conectar fácilmente en cascada con otros circuitos de filtro activos para dar diseños de filtros más complejos.

La respuesta de frecuencia normalizada del filtro de paso bajo de segundo orden es fijada por la red RC y es generalmente idéntica a la del tipo de primer orden. La principal diferencia entre un primero y segundo filtro de paso bajo orden es que la banda de parada de roll-off será dos veces los filtros de orden 1º en 40 dB / década (12 dB / octava) como la frecuencia de funcionamiento aumenta por encima de la línea del punto de corte de frecuencia, ƒc como se muestra:

Respuesta de frecuencia de paso bajo normalizada

El diagrama de Bode de respuesta de frecuencia anterior es básicamente el mismo que el de un filtro de primer orden. La diferencia esta vez es la inclinación de la caída, que es de -40dB / década en la banda de parada. Sin embargo, los filtros de segundo orden pueden exhibir una variedad de respuestas dependiendo del factor de aumento de voltaje de los circuitos, Q en el punto de frecuencia de corte.

En los filtros activos de segundo orden,el factor de amortiguación, ζ (zeta), que es el inverso de Q. normalmente se utiliza tanto Q como ζ están determinados independientemente por la ganancia del amplificador, A de modo que a medida que Q disminuye, aumenta el factor de amortiguación. En términos simples, un filtro de paso bajo siempre será de paso bajo por su naturaleza, pero puede exhibir un pico resonante en las proximidades de la frecuencia de corte, es decir, la ganancia puede aumentar rápidamente debido a los efectos de resonancia de la ganancia de los amplificadores.

Entonces el factor de calidad Q, representa el “peakiness” de este pico de resonancia, que es su altura y estrechez alrededor del punto de corte de frecuencia, ƒC. Pero la ganancia de un filtro también determina la cantidad de su retroalimentación y, por lo tanto, tiene un efecto significativo en la respuesta de frecuencia del filtro.

Por lo general, para mantener la estabilidad, la ganancia de un filtro activo no debe ser superior a 3 y se expresa mejor como:

Factor de calidad, «Q»

Entonces podemos ver que la ganancia de los filtros, A para una configuración de amplificador no inversor debe estar entre 1 y 3 (el factor de amortiguación, ζ entre cero y 2). Por lo tanto, valores más altos de Q o valores más bajos de ζ dan un pico mayor a la respuesta y una tasa de caída inicial más rápida, como se muestra:

Respuesta de amplitud del filtro de segundo orden

La respuesta de amplitud del filtro de paso bajo de segundo orden varía para diferentes valores del factor de amortiguación, ζ. Cuando ζ = 1.0 o más (2 es el máximo), el filtro se convierte en lo que se llama “sobreamortiguado” con la respuesta de frecuencia mostrando una curva plana larga. Cuando ζ = 0, la salida de los filtros alcanza un pico pronunciado en el punto de corte que se asemeja a un punto agudo en el que se dice que el filtro está «subamortiguado».

Entonces, en algún punto intermedio, ζ = 0 y ζ = 2.0, debe haber un punto donde la respuesta de frecuencia sea del valor correcto, y lo hay. Esto es cuando el filtro está «críticamente amortiguado» y ocurre cuando ζ = 0,7071.

Una nota final, cuando la cantidad de retroalimentación alcanza 4 o más, el filtro comienza a oscilar por sí mismo en el punto de frecuencia de corte debido a los efectos de resonancia, convirtiendo el filtro en un oscilador. Este efecto se llama auto oscilación. Luego, para un filtro de segundo orden de paso bajo, tanto Q como ζ juegan un papel crítico.

Podemos ver en las curvas de respuesta de frecuencia normalizadas anteriores para un filtro de primer orden (línea roja) que la ganancia de la banda de paso permanece plana y nivelada (llamada máximamente plana) hasta que la respuesta de frecuencia alcanza el punto de frecuencia de corte cuando: ƒ = ƒr y la ganancia del filtro se reduce más allá de su frecuencia de esquina a 1 / √2, o 0,7071 de su valor máximo. Este punto se conoce generalmente como el punto de-3dB y para un filtro de paso bajo de primer orden, el factor de amortiguación será igual a uno, ( ζ = 1 ).

Sin embargo, este punto de corte de -3dB estará en una posición de frecuencia diferente para los filtros de segundo orden debido a la tasa de caída más pronunciada de -40dB / década (línea azul). En otras palabras, la frecuencia de esquina, ƒr cambia de posición a medida que aumenta el orden del filtro. Luego, para volver a colocar los filtros de segundo orden -3dB en la misma posición que los filtros de primer orden, debemos agregar una pequeña cantidad de ganancia al filtro.

Entonces, para un diseño de filtro de paso bajo de segundo orden de Butterworth, la cantidad de ganancia sería: 1.586, para un diseño de filtro de segundo orden de Bessel: 1.268, y para un diseño de paso bajo de Chebyshev: 1.234.

Ejemplo de filtro de segundo orden No.1

Un filtro de paso bajo de segundo orden debe diseñarse alrededor de un amplificador operacional no inversor con valores iguales de resistencia y condensador en su circuito de determinación de frecuencia de corte. Si las características de los filtros se dan como: Q = 5y ƒc = 159Hz, diseñe un filtro de paso bajo adecuado y dibuje su respuesta de frecuencia.

Características dadas: R1 = R2, C1 = C2, Q = 5 y ƒc = 159Hz

Del circuito anterior sabemos que para resistencias y capacitancias iguales, el punto de frecuencia de corte, ƒc se da como:

Al elegir un valor adecuado de, por ejemplo, 10 kΩ para las resistencias, el valor del condensador resultante se calcula como:

Luego, para una frecuencia de esquina de corte 159Hz, R = 10kΩ y C = 0.1uF.

con un valor de Q = 5, la ganancia de los filtros A se calcula como:

Sabemos desde arriba que la ganancia de un amplificador operacional no inversor se da como:

Por lo tanto, el circuito final para el filtro de paso bajo de segundo orden se da como:

Circuito de filtro de paso bajo de segundo orden

Podemos ver que el pico de la curva de respuesta de frecuencia es bastante nítido en la frecuencia de corte debido al valor del factor de alta calidad, Q = 5. En este punto, la ganancia del filtro se da como: Q × A = 14, o aproximadamente + 23dB, una gran diferencia del valor calculado de 2.8, (+ 8.9dB).

Pero muchos libros, como el de la derecha, nos dicen que la ganancia del filtro en el punto de frecuencia de corte normalizado, etc, debería estar en el punto -3dB. Al reducir el valor de Q significativamentea a un valor de 0,7071, se obtiene una ganancia de, A = 1,586 y una respuesta de frecuencia que es máximamente plana en la banda de paso con una atenuación de -3dB en el punto de corte igual que para una respuesta de filtro Butterworth de segundo orden.

Hasta ahora, hemos visto que los filtros de segundo orden pueden tener su punto de frecuencia de corte establecido en cualquier valor deseado, pero se puede alejar de este valor deseado mediante el factor de amortiguación, ζ. Los diseños de filtros activos permiten que el orden del filtro varíe hasta cualquier valor, dentro de lo razonable, mediante la conexión en cascada de las secciones del filtro.

En la práctica, al diseñar un filtro de paso bajo de orden n-ésimo, es deseable establecer la frecuencia de corte para la sección de primer orden (si el orden del filtro es impar) y establecer el factor de amortiguación y la ganancia correspondiente para cada una de las secciones de segundo orden para que se obtenga la respuesta general correcta. Para que el diseño de filtros de paso bajo sea más fácil de lograr, los valores de ζ, Q y A están disponibles en forma tabulada para filtros activos, como veremos en el tutorial del filtro Butterworth. Veamos otro ejemplo.

Ejemplo de filtro de segundo orden No.2

Diseñe un filtro de paso bajo de segundo orden no inversor que tendrá las siguientes características de filtro: Q = 1y ƒc = 79,5Hz.

Desde arriba, la frecuencia de esquina, ƒc del filtro se da como:

Al elegir un valor adecuado de 1 kΩ para las resistencias de los filtros, los valores de los condensadores resultantes se calculan como:

Por lo tanto, para una frecuencia de esquina de 79.5Hz, o 500 rads / s, R = 1kΩ y C = 2.0uF.

Con un valor de Q = 1 dado, la ganancia de filtros A se calcula de la siguiente manera:

La ganancia de voltaje para un circuito de amplificador operacional no inversor se proporcionó anteriormente como:

Por lo tanto, el circuito de filtro de paso bajo de segundo orden que tiene una Q de 1 y una frecuencia de esquina de 79,5 Hz se da como:

Circuito de filtro de paso bajo 

Filtro de paso alto de segundo orden

Hay muy poca diferencia entre la configuración del filtro de paso bajo de segundo orden y la configuración de filtro de paso alto de segundo orden, lo único que ha cambiado es la posición de las resistencias y los condensadores como se muestra:

Filtro de paso alto de segundo orden

Dado que los filtros de paso alto y paso bajo de segundo orden son los mismos circuitos, excepto que las posiciones de las resistencias y los condensadores se intercambian, el diseño y los procedimientos de escalado de frecuencia para el filtro de paso alto son exactamente los mismos que los del filtro de paso bajo anterior. Entonces, el diagrama de Bode para un filtro de paso alto de segundo orden se da como:

Respuesta de frecuencia de paso alto normalizada

Al igual que con el filtro de paso bajo anterior, la inclinación de la caída en la banda de parada es de -40 dB / década.

En los dos circuitos anteriores, el valor de la ganancia de voltaje del amplificador operacional, ( Av ) lo establece la red de retroalimentación de los amplificadores. Esto solo establece la ganancia para las frecuencias dentro de la banda de paso del filtro. Podemos elegir para amplificar la salida y ajustar este valor de ganancia por cualquier cantidad es adecuada para nuestro propósito y definir esta ganancia como una constante, K.

Los filtros Sallen-Key de segundo orden también se conocen como filtros de retroalimentación positiva, ya que la salida se retroalimenta al terminal positivo del amplificador operacional. Este tipo de diseño de filtro activo es popular porque requiere solo un amplificador operacional, lo que lo hace relativamente económico.