La característica principal de un filtro de paso de banda o cualquier filtro para el caso, es su capacidad para pasar frecuencias relativamente sin atenuar sobre una banda específica o una extensión de frecuencias llamada «banda de paso».
Para un filtro de paso bajo, el paso comienza desde 0Hz o CC y continúa hasta el punto de frecuencia de corte especificado a -3dB por debajo de la ganancia máxima de la banda de paso. Del mismo modo, para un filtro de paso alto, la banda de paso comienza desde esta frecuencia de corte de -3dB y continúa hasta el infinito o la ganancia máxima de bucle abierto para un filtro activo.
Sin embargo, el filtro de paso de banda activo es ligeramente diferente en que es un circuito de filtro selectivo de frecuencia utilizado en sistemas electrónicos para separar una señal en una frecuencia particular, o un rango de señales que se encuentran dentro de una cierta «banda» de frecuencias de señales en todas las demás frecuencias. Esta banda o rango de frecuencias se establece entre dos puntos de frecuencia de corte o de esquina etiquetados como “frecuencia más baja” ( ƒL ) y “frecuencia más alta” ( ƒH ) mientras atenúa cualquier señal fuera de estos dos puntos.
El filtro simple de paso de banda activo se puede hacer fácilmente conectando en cascada un solo filtro de paso bajo con un solo filtro de paso alto, como se muestra:

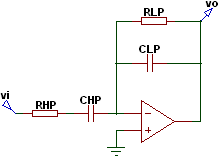
La frecuencia de corte o esquina del filtro de paso bajo (LPF) es más alta que la frecuencia de corte del filtro de paso alto (HPF) y la diferencia entre las frecuencias en el punto -3dB determinará el «ancho de banda» del filtro de paso de banda mientras atenúa cualquier señal fuera de estos puntos. Una forma de hacer un filtro simple de paso de banda activo es conectar los filtros pasivos básicos de paso alto y paso bajo que miramos anteriormente a un circuito amplificador operacional como se muestra:
Contenido
Circuito de filtro de paso de banda activo

Esta conexión en cascada de los filtros pasivos individuales de paso alto y bajo produce un circuito de filtro de tipo “factor Q” bajo que tiene una banda de paso ancho. La primera etapa del filtro será la etapa de paso alto que utiliza el condensador para bloquear cualquier polarización de CC de la fuente. Este diseño tiene la ventaja de producir una respuesta de frecuencia de banda de paso asimétrica relativamente plana con la mitad representando la respuesta de paso bajo y la otra mitad representando la respuesta de paso alto como se muestra:

El punto de esquina superior ( ƒH ) así como el punto de corte de frecuencia de esquina inferior ( ƒL ) se calculan de la misma forma que antes en los circuitos de filtro de paso alto y bajo de primer orden estándar. Obviamente, se requiere una separación razonable entre los dos puntos de corte para evitar cualquier interacción entre las etapas de paso bajo y paso alto. El amplificador también proporciona aislamiento entre las dos etapas y define la ganancia de voltaje general del circuito.
El ancho de banda del filtro es, por lo tanto, la diferencia entre estos puntos superior e inferior de -3dB. Por ejemplo, suponga que tenemos un filtro de paso de banda cuyos puntos de corte de -3dB se establecen en 200Hz y 600Hz. Entonces, el ancho de banda del filtro se daría como: Ancho de banda (BW) = 600 – 200 = 400Hz.
La respuesta de frecuencia normalizada y el desplazamiento de fase para un filtro de paso de banda activo serán los siguientes:
Respuesta de frecuencia de paso de banda activa

Si bien el circuito de filtro sintonizado pasivo anterior funcionará como un filtro de paso de banda, la banda de paso (ancho de banda) puede ser bastante amplia y esto puede ser un problema si queremos aislar una pequeña banda de frecuencias. El filtro de paso de banda activo también se puede hacer usando un amplificador operacional inversor.
Entonces, al reorganizar las posiciones de las resistencias y los capacitores dentro del filtro, podemos producir un circuito de filtro mucho mejor, como se muestra a continuación. Para un filtro de paso de banda activo, el punto de corte inferior -3dB viene dado por ƒC1 mientras que el punto de corte superior -3dB viene dado por ƒC2.
Circuito de filtro de paso de banda inversora


Este tipo de filtro de paso de banda está diseñado para tener una banda de paso mucho más estrecha. La frecuencia central y el ancho de banda del filtro están relacionados con los valores de R1, R2, C1 y C2. La salida del filtro se toma nuevamente de la salida del amplificador operacional.
Filtro activo de paso de banda de retroalimentación múltiple
Podemos mejorar la respuesta de paso de banda del circuito anterior reorganizando los componentes nuevamente para producir un filtro de paso de banda de retroalimentación múltiple de ganancia infinita (IGMF). Este tipo de diseño de paso de banda activo produce un circuito «sintonizado» basado en un filtro activo de retroalimentación negativa que le da una respuesta de amplitud de «factor Q» alto (hasta 25) y una caída pronunciada a ambos lados de su frecuencia central. Debido a que la respuesta de frecuencia del circuito es similar a un circuito de resonancia, esta frecuencia central se conoce como frecuencia resonante, ( ƒr ). Considere el circuito a continuación:
Filtro activo de retroalimentación múltiple de ganancia infinita

Este circuito de filtro de paso de banda activo utiliza la ganancia total del amplificador operacional, con retroalimentación negativa múltiple aplicada a través de la resistencia, R2 y el condensador C2. Entonces podemos definir las características del filtro IGMF de la siguiente manera:

Podemos ver entonces que la relación entre las resistencias, R1 y R2 determina el “factor Q” de paso de banda y la frecuencia a la que ocurre la amplitud máxima, la ganancia del circuito será igual a -2Q2. Luego, a medida que aumenta la ganancia, también lo hace la selectividad. En otras palabras, alta ganancia – alta selectividad.
Ejemplo de filtro de paso de banda activo No.1
Un filtro de paso de banda activo que tiene una ganancia de voltaje Av de uno (1) y una frecuencia resonante, ƒr de 1 kHz se construye utilizando un circuito de filtro de retroalimentación múltiple de ganancia infinita. Calcule los valores de los componentes necesarios para implementar el circuito.
En primer lugar, podemos determinar los valores de las dos resistencias, R1 y R2 necesarios para el filtro activo, utilizando la ganancia del circuito para encontrar Q de la siguiente manera.

Entonces podemos ver que un valor de Q = 0.7071 da una relación de resistencia, R2 siendo el doble del valor de la resistencia R1. Entonces podemos elegir cualquier valor adecuado de resistencias para dar la relación requerida de dos. Entonces la resistencia R1 = 10kΩ y R2 = 20kΩ.
La frecuencia central o resonante se da como 1 kHz. Usando los nuevos valores de resistencia obtenidos, podemos determinar el valor de los capacitores requeridos asumiendo que C = C1 = C2.

El valor estándar más cercano es 10 nF.
Punto de frecuencia resonante
La forma real de la curva de respuesta de frecuencia para cualquier filtro de paso de banda pasivo o activo dependerá de las características del circuito de filtro con la curva anterior definida como una respuesta de paso de banda «ideal». Un filtro de paso de banda activo es un filtro de tipo de segundo orden porque tiene «dos» componentes reactivos (dos condensadores) dentro de su diseño de circuito.
Como resultado de estos dos componentes reactivos, el filtro tendrá una respuesta de pico o Frecuencia Resonante ( ƒr ) en su “frecuencia central”, ƒc. La frecuencia central generalmente se calcula como la media geométrica de las dos frecuencias de -3dB entre los puntos de corte superior e inferior con la frecuencia resonante (punto de oscilación) dada como:

- Donde:
- ƒr es la frecuencia resonante o central
- ƒL es el punto de frecuencia de corte inferior de -3dB
- ƒH es el punto de frecuencia de corte superior de -3db
Y, en nuestro ejemplo simple en el texto anterior, los puntos de corte de -3dB inferior y superior de los filtros están a 200Hz y 600Hz respectivamente, entonces la frecuencia central resonante del filtro de paso de banda activo sería:

El «Q» o factor de calidad
En un circuito de filtro de paso de banda, el ancho total de la banda de paso real entre los puntos de esquina superior e inferior de -3dB del filtro determina el factor de calidad o punto Q del circuito. Este factor Q es una medida de cuán «selectivo» o «no selectivo» es el filtro de paso de banda hacia una determinada distribución de frecuencias. Cuanto menor sea el valor del factor Q, mayor será el ancho de banda del filtro y, en consecuencia, cuanto mayor sea el factor Q, más estrecho y “selectivo” será el filtro.
El factor de calidad, Q del filtro a veces recibe el símbolo griego de Alfa, ( α ) y se conoce como la frecuencia de pico alfa donde:

Dado que el factor de calidad de un filtro de paso de banda activo (sistema de segundo orden) se relaciona con la «nitidez» de la respuesta de los filtros alrededor de su frecuencia resonante central ( ƒr ), también se puede considerar como el «factor de amortiguación» o el «coeficiente de amortiguación». Porque cuanto más amortiguación tiene el filtro, más plana es su respuesta y, del mismo modo, cuanto menos amortiguación tiene el filtro, más nítida es su respuesta. A la relación de amortiguación se le da el símbolo griego de Xi, ( ξ ) donde:

La «Q» de un filtro de paso de banda es la relación entre la frecuencia de, ( resonancia ƒr ) y el ancho de banda, ( BW ) entre las frecuencias superior e inferior de -3dB y se da como:
 |  |
Entonces, para nuestro ejemplo simple anterior, si el ancho de banda (BW) es 400Hz, eso es ƒH – ƒL, y la frecuencia resonante central, ƒr es 346Hz. Entonces, el factor de calidad “Q” del filtro de paso de banda se dará como:
346Hz / 400Hz = 0.865. Tenga en cuenta que Q es una proporción, no tiene unidades.
Al analizar filtros activos, generalmente se considera un circuito normalizado que produce una respuesta de frecuencia “ideal” que tiene una forma rectangular, y una transición entre la banda de paso y la banda de parada que tiene una pendiente de caída abrupta o muy pronunciada. Sin embargo, estas respuestas ideales no son posibles en el mundo real, por lo que usamos aproximaciones para darnos la mejor respuesta de frecuencia posible para el tipo de filtro que estamos tratando de diseñar.
Probablemente la aproximación de filtro más conocida para hacer esto es el Butterworth o filtro de respuesta máxima plana. En el siguiente tutorial veremos filtros de orden superior y usaremos aproximaciones de Butterworth para producir filtros que tengan una respuesta de frecuencia que sea lo más plana posible matemáticamente en la banda de paso y una transición suave o tasa de caída.