Filtro de paso bajo activo

En los tutoriales de filtro pasivo de RC, vimos cómo un circuito de filtro básico de primer orden, como el Los filtros de paso bajo y de paso alto se pueden hacer usando solo una resistencia en serie con un capacitor no polarizado conectado a través de una señal de entrada sinusoidal.

También notamos que la principal desventaja de los filtros pasivos es que la amplitud de la señal de salida es menor que la de la señal de entrada, es decir, la ganancia nunca es mayor que la unidad y que la impedancia de carga afecta las características de los filtros.

Con circuitos de filtro pasivo que contienen múltiples etapas, esta pérdida en la amplitud de la señal llamada «Atenuación» puede volverse grave y silenciosa. Una forma de restaurar o controlar esta pérdida de señal es mediante el uso de amplificación mediante el uso de filtros activos.

Como su nombre lo indica, los filtros activos contienen componentes activos como amplificadores operacionales, transistores o FET dentro de su diseño de circuito. Obtienen su energía de una fuente de energía externa y la usan para aumentar o amplificar la señal de salida.

La amplificación de filtro también se puede utilizar para dar forma o alterar la respuesta de frecuencia del circuito de filtro produciendo una respuesta de salida más selectiva, haciendo que el ancho de banda de salida del filtro sea más estrecho o incluso más ancho. Entonces, la principal diferencia entre un «filtro pasivo» y un «filtro activo» es la amplificación.

Un filtro activo generalmente usa un amplificador operacional (amplificador operacional) dentro de su diseño y en el tutorial del amplificador operacional vimos que un amplificador operacional tiene una impedancia de entrada alta, una impedancia de salida baja y una ganancia de voltaje determinada por la red de resistencias dentro de su Bucle de retroalimentación.

A diferencia de un filtro de paso alto pasivo que en teoría tiene una respuesta de alta frecuencia infinita, la respuesta de frecuencia máxima de un filtro activo se limita al producto de ganancia / ancho de banda (o ganancia de bucle abierto) del amplificador operacional que se está utilizando. Aún así, los filtros activos son generalmente mucho más fáciles de diseñar que los filtros pasivos, producen buenas características de rendimiento, muy buena precisión con una caída pronunciada y poco ruido cuando se usan con un buen diseño de circuito.

Filtro de paso bajo activo

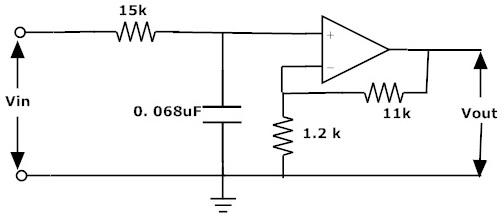
El filtro activo más común y de fácil comprensión es el filtro de paso bajo activo. Su principio de funcionamiento y respuesta de frecuencia es exactamente el mismo que el del filtro pasivo visto anteriormente, la única diferencia esta vez es que usa un amplificador operacional para amplificación y control de ganancia. La forma más simple de un filtro activo de paso bajo es conectar un amplificador inversor o no inversor, los mismos que se discutieron en el tutorial del amplificador operacional, al circuito de filtro de paso bajo RC básico como se muestra:

Filtro de paso bajo de primer orden

Este filtro activo de paso bajo de primer orden consiste simplemente en una etapa de filtro RC pasivo que proporciona una ruta de baja frecuencia a la entrada de un amplificador operacional no inversor. El amplificador está configurado como seguidor de voltaje (búfer), lo que le da una ganancia de CC de uno, Av = +1 o ganancia unitaria en comparación con el filtro RC pasivo anterior que tiene una ganancia CC de menos de la unidad.

La ventaja de esta configuración es que la alta impedancia de entrada de los amplificadores operacionales evita una carga excesiva en la salida de los filtros, mientras que su baja impedancia de salida evita que el punto de frecuencia de corte de los filtros se vea afectado por cambios en la impedancia de la carga.

Si bien esta configuración proporciona una buena estabilidad al filtro, su principal desventaja es que no tiene una ganancia de voltaje por encima de uno. Sin embargo, aunque la ganancia de voltaje es la unidad, la ganancia de potencia es muy alta ya que su impedancia de salida es mucho menor que su impedancia de entrada. Si se requiere una ganancia de voltaje mayor que uno, podemos usar el siguiente circuito de filtro.

Filtro de paso bajo activo con amplificación

La respuesta de frecuencia del circuito será la misma que la del filtro RC pasivo, excepto que la amplitud de la salida aumenta con la ganancia de la banda de paso, AF del amplificador. Para un circuito amplificador no inversor, la magnitud de la ganancia de voltaje para el filtro se da como una función de la resistencia de retroalimentación ( R2 ) dividida por su valor de resistencia de entrada correspondiente ( R1 ) y se da como:

Por lo tanto, la ganancia de un filtro de paso bajo activo en función de la frecuencia será:

Ganancia de un filtro de paso bajo de primer orden

• Donde:
•   AF = la ganancia de banda de paso del filtro, (1 + R2 / R1)
•   ƒ = la frecuencia de la señal de entrada en hercios, (Hz)
•   ƒc = la frecuencia de corte en Hertz, (Hz)

Por lo tanto, el funcionamiento de un filtro activo de paso bajo se puede verificar a partir de la ecuación de ganancia de frecuencia anterior como:

• 1. A frecuencias muy bajas, ƒ <ƒc

• 2. En el corte fuera de frecuencia, ƒ = ƒc

• 3. A frecuencias muy altas, ƒ> ƒc

Por lo tanto, el filtro de paso bajo activo tiene una ganancia constante aF desde 0 Hz a la alta frecuencia de corte punto, ƒC.En ƒC, la ganancia es de 0.707AF, y después de ƒC disminuye a una tasa constante a medida que aumenta la frecuencia. Es decir, cuando la frecuencia se multiplica por diez (una de cada), la ganancia de voltaje se divide por 10.

En otras palabras, la ganancia disminuye 20 dB (= 20 * log (10)) cada vez que la frecuencia aumenta en 10. Cuando se trata de con circuitos de filtro, la magnitud de la ganancia de banda de paso del circuito se expresa generalmente en decibelios o dB en función de la ganancia de voltaje, y esto se define como:

Magnitud de ganancia de voltaje en (dB)

Ejemplo de filtro de paso bajo activo No.1

Diseñe un circuito de filtro de paso bajo activo no inversor que tenga una ganancia de diez a bajas frecuencias, un corte de alta frecuencia o una frecuencia de esquina de 159Hz y una impedancia de entrada de 10KΩ.

La ganancia de voltaje de un amplificador operacional no inversor se da como:

Suponga que un valor para la resistencia R1 de 1kΩ reordenando la fórmula anterior da un valor para R2 de:

Entonces, para una ganancia de voltaje de 10, R1 = 1kΩ y R2 = 9kΩ. Sin embargo, una resistencia de 9kΩ no existe lo que el siguiente valor preferido de 9k1Ω se utiliza en su lugar. La conversión de esta ganancia de voltaje a un valor equivalente en decibelios dB da:

La frecuencia de corte o de esquina (ƒc) se da como 159Hz con una impedancia de entrada de 10kΩ. Esta frecuencia de corte se puede encontrar usando la fórmula:

Dónde ƒc = 159Hz y R = 10kΩ.

Al reorganizar la fórmula estándar anterior, podemos encontrar el valor del condensador de filtro C como:

Así, el circuito de filtro de paso bajo final junto con su respuesta de frecuencia se da a continuación como:

Circuito de filtro de paso bajo

Curva de respuesta de frecuencia

Si cambia la impedancia externa conectada a la entrada del circuito del filtro, este cambio de impedancia también afectaría la frecuencia de esquina del filtro (componentes conectados entre sí en serie o en paralelo). Una forma de evitar cualquier influencia externa es colocar el capacitor en paralelo con la resistencia de retroalimentación R2 eliminándolo efectivamente de la entrada pero manteniendo las características de los filtros.

Sin embargo, el valor del condensador cambiará ligeramente de 100nF a 110nF para tener en cuenta la resistencia de 9k1Ω, pero la fórmula utilizada para calcular la frecuencia de corte es la misma que la utilizada para el filtro de paso bajo pasivo RC.

Ejemplos de diferentes circuitos de filtros de paso bajo activo de primer orden, se dan configuraciones de:

Circuito de filtro de amplificador inversor simplificado

Aquí, el condensador se ha movido de la entrada de amplificadores operacionales a su circuito de retroalimentación en paralelo con R2. Esta combinación paralela de C y R2 establece el punto -3dB como antes, pero permite que la ganancia de los amplificadores disminuya indefinidamente más allá de la frecuencia de esquina.

A bajas frecuencias, la reactancia de los condensadores es mucho más alta que R2, por lo que la ganancia de CC se establece mediante la fórmula inversora estándar de: -R2 / R1 = 10, para este ejemplo. A medida que aumenta la frecuencia, la reactancia de los capacitores disminuye reduciendo la impedancia de la combinación en paralelo de Xc || R2, hasta que finalmente, a una frecuencia lo suficientemente alta, Xc se reduce a cero.

La ventaja aquí es que la impedancia de entrada de los circuitos ahora es solo R1 y la señal de salida está invertida. Con los componentes que determinan la frecuencia de esquina en el circuito de retroalimentación, el punto de ajuste RC no se ve afectado por variaciones en la impedancia de la fuente y la ganancia de CC se puede ajustar independientemente de la frecuencia de esquina.

Circuito de filtro de amplificador no inversor de ganancia unitaria

Aquí, debido a la posición del capacitor en paralelo con la resistencia de retroalimentación R2, la frecuencia de esquina de paso bajo se establece como antes, pero a altas frecuencias la reactancia del capacitor domina el cortocircuito R2 reduciendo la ganancia del amplificador . A una frecuencia lo suficientemente alta, la ganancia llega a la unidad (0dB) ya que el amplificador se convierte efectivamente en un seguidor de voltaje, por lo que la ecuación de ganancia se convierte en 1 + 0 / R1 que es igual a 1 (unidad).

Las aplicaciones de los filtros de paso bajo activo se encuentran en amplificadores de audio, ecualizadores o sistemas de altavoces para dirigir las señales de graves de baja frecuencia a los altavoces de graves más grandes o para reducir cualquier ruido de alta frecuencia o distorsión de tipo «silbido». Cuando se usa así en aplicaciones de audio, el filtro de paso bajo activo a veces se denomina filtro de “refuerzo de graves”.

Filtro activo de paso bajo de segundo orden

Al igual que con el filtro pasivo, un filtro activo de paso bajo de primer orden se puede convertir en un filtro de paso bajo de segundo orden simplemente usando una red adicional RC en la ruta de entrada. La respuesta de frecuencia del filtro de paso bajo de segundo orden es idéntica a la del tipo de primer orden, excepto que la atenuación de la banda de parada será el doble de los filtros de primer orden a 40 dB / década (12 dB / octava). Por lo tanto, los pasos de diseño requeridos del filtro de paso bajo activo de segundo orden son los mismos.

Circuito de filtro de paso bajo activo de segundo orden

Cuando se conectan en cascada circuitos de filtro para formar filtros de orden superior, la ganancia total del filtro es igual al producto de cada etapa. Por ejemplo, la ganancia de una etapa puede ser 10 y la ganancia de la segunda etapa puede ser 32 y la ganancia de una tercera etapa puede ser 100. Entonces la ganancia total será 32,000, (10 x 32 x 100) como se muestra a continuación.

Ganancia de voltaje en cascada

Los filtros activos de segundo orden (dos polos) son importantes porque los filtros de orden superior se pueden diseñar con ellos. Al conectar en cascada filtros de primer y segundo orden, se pueden construir filtros con un valor de orden, ya sea impar o incluso hasta cualquier valor. En el siguiente tutorial sobre filtros, veremos que los filtros de paso alto activos se pueden construir invirtiendo las posiciones de la resistencia y el condensador en el circuito.