El filtro de paso de banda pasiva se puede hacer conectando un filtro de paso bajo con un filtro de paso alto.
Los filtros de paso de banda se pueden usar para aislar o filtrar ciertas frecuencias que se encuentran dentro de una banda o rango de frecuencias en particular. La frecuencia de corte o el punto ƒc en un filtro simple pasivo RC, se puede controlar con precisión usando una sola resistencia en serie con un capacitor no polarizado, y dependiendo de la forma en que estén conectados, hemos visto que un paso bajo o se obtiene un filtro de paso alto.
Un uso simple de estos tipos de filtros pasivos es en aplicaciones o circuitos de amplificadores de audio, como filtros de cruce de altavoces o controles de tono del preamplificador. A veces es necesario pasar solo un cierto rango de frecuencias que no comienzan en 0Hz, (DC) o terminan en algún punto superior de alta frecuencia, pero que están dentro de un cierto rango o banda de frecuencias, ya sea estrecha o ancha.
Al conectar o «conectar en cascada» un solo circuito de filtro de paso bajo con un circuito de filtro de paso alto polo pp podemos producir otro tipo de filtro RC pasivo que pasa un rango seleccionado o «banda» de frecuencias que pueden ser angostas o anchas mientras atenúa todas los que están fuera de este rango. Este nuevo tipo de disposición de filtro pasivo produce un filtro selectivo de frecuencia conocido comúnmente como filtro de paso de banda o BPF para abreviar.
Contenido
Circuito de filtro de paso de banda

A diferencia del filtro de paso bajo que solo pasa señales de un rango de baja frecuencia o el filtro de paso alto que pasa señales de un rango de frecuencia más alto, un filtro de paso de banda pasa señales dentro de una cierta «banda» o «dispersión» de frecuencias sin distorsionar la entrada señal o la introducción de ruido adicional. Esta banda de frecuencias puede tener cualquier ancho y se conoce comúnmente como filtros de ancho de banda.
El ancho de banda se define comúnmente como el rango de frecuencia que existe entre dos puntos de corte de frecuencia especificados ( ƒc ), que están 3dB por debajo del centro máximo o pico resonante mientras atenúa o debilita los otros puntos fuera de estos dos puntos.
Luego, para frecuencias muy extendidas, podemos simplemente definir el término «ancho de banda», BW como la diferencia entre la frecuencia de corte más baja ( ƒcLOWER ) y las frecuencias de corte más alta ( ƒcHIGHER ). En otras palabras, BW = ƒH – ƒL. Claramente, para que un filtro de banda de paso funcione correctamente, la frecuencia de corte del filtro de paso bajo debe ser más alta que la frecuencia de corte del filtro de paso alto.
El «ideal» filtro de paso de banda también se puede utilizar para aislar o filtrar ciertas frecuencias que se encuentran dentro de una banda de frecuencias en particular, por ejemplo, cancelación de ruido. Los filtros de paso de banda se conocen generalmente como filtros de segundo orden (bipolares) porque tienen «dos» componentes reactivos, los condensadores, dentro de su diseño de circuito. Un condensador en el circuito de paso bajo y otro condensador en el circuito de paso alto.
Respuesta de frecuencia de un filtro de paso de banda de segundo orden

El diagrama de Bode o la curva de respuesta de frecuencia anterior muestra las características del filtro de paso de banda. Aquí la señal se atenúa a bajas frecuencias con la salida aumentando a una pendiente de + 20 dB / de cada (6 dB / octava) hasta que la frecuencia alcanza el “corte inferior” punto de ƒL. A esta frecuencia, el voltaje de salida es nuevamente 1 / √2 = 70.7% del valor de la señal de entrada o -3dB (20 * log (VOUT/ VIN)) de la entrada.
La salida continúa con la ganancia máxima hasta que alcanza el punto de “corte superior” ƒH donde la salida disminuye a una tasa de -20dB / de cada (6dB / Octava) atenuando cualquier señal de alta frecuencia. El punto de máxima ganancia de salida es generalmente la media geométrica del valor de dos -3dB entre los puntos de corte inferior y superior y se denomina valor de “frecuencia central” o “pico resonante” ƒr. Este valor de la media geométrica se calcula como ƒr 2 = ƒ(SUPERIOR) x ƒ(INFERIOR).
Un filtro de paso de banda se considera un filtro de tipo de segundo orden (dos polos) porque tiene «dos» componentes reactivos dentro de la estructura de su circuito, entonces el ángulo de fase será el doble que el de los filtros de primer orden vistos anteriormente, es decir, 180°. El ángulo de fase de la señal de salida LLEVA al de la entrada en +90° hasta el centro o la frecuencia resonante, ƒr donde se convierte en «cero» grados (0°) o «en fase» y luego cambia a LAG la entrada en -90° a medida que aumenta la frecuencia de salida.
Los puntos de frecuencia de corte superior e inferior para un filtro de paso de banda se pueden encontrar utilizando la misma fórmula que para los filtros de paso alto y bajo, por ejemplo.

Entonces, claramente, el ancho de la banda de paso del filtro se puede controlar mediante el posicionamiento de los dos puntos de frecuencia de corte de los dos filtros.
Ejemplo de filtro de paso de banda No.1
Un segundo orden del filtro de paso de banda se construirá utilizando componentes RC que solo permitirán que un rango de frecuencias pase por encima de 1 kHz (1,000 Hz) y por debajo de 30 kHz (30,000 Hz). Suponiendo que ambas resistencias tengan valores de 10 kΩ, calcule los valores de los dos condensadores requeridos.
La etapa de filtro de paso alto
El valor del capacitor C1 requerido para dar una frecuencia de corte ƒL de 1kHz con un valor de resistencia de 10kΩ se calcula como:

Entonces, los valores de R1 y C1 requeridos para que la etapa de paso alto dé una frecuencia de corte de 1.0kHz son: R1 = 10kΩ y al valor preferido más cercano, C1 = 15nF.
La etapa de filtro de paso bajo
El valor del capacitor C2 requerido para dar una frecuencia de corte ƒH de 30kHz con un valor de resistencia de 10kΩ se calcula como:

Entonces, los valores de R2 y C2 requeridos para que la etapa de paso bajo dé una frecuencia de corte de 30kHz son, R = 10kΩ y C = 530pF. Sin embargo, el valor preferido más cercano del valor calculado del condensador de 530pF es 560pF, por lo que se usa en su lugar.
Con los valores de las resistencias R1 y R2 dados como 10kΩ, y los dos valores de los condensadores C1 y C2 encontrados para los filtros de paso alto y paso bajo como 15nF y 560pF respectivamente, entonces el circuito para nuestro simple filtro de paso de banda pasiva se da como:
Circuito de filtro de paso de banda completo

Frecuencia resonante del filtro de paso de banda
También podemos calcular el“frecuencia resonante” o “frecuencia central” (ƒrpunto de) del filtro de paso de banda donde la ganancia de salida está en su valor máximo o pico. Este valor máximo no es el promedio aritmético de los puntos de corte superior e inferior de -3dB como cabría esperar, sino que de hecho es el valor «geométrico» o medio. Este valor medio geométrico se calcula como ƒr 2 = ƒc(SUPERIOR) x ƒc(INFERIOR) por ejemplo:
Ecuación de frecuencia central

- Donde, ƒr es la frecuencia resonante o central
- ƒL es el punto de frecuencia de corte inferior de -3dB
- ƒH es el punto de frecuencia de corte superior de -3db
Y en nuestro ejemplo simple anterior, se encontró que las frecuencias de corte calculadas eran ƒL = 1,060 Hz y ƒH = 28,420 Hz usando los valores del filtro.
Luego, al sustituir estos valores en la ecuación anterior, se obtiene una frecuencia resonante central de:

Resumen del filtro de paso de banda pasiva
Un simple filtro de paso de banda pasiva se puede hacer conectando en cascada un solo filtro de paso bajo con un filtro de paso alto. El rango de frecuencia, en hercios, entre los puntos de corte inferior y superior de -3dB de la combinación RC se conoce como los filtros “Ancho de banda”.
El ancho o rango de frecuencia del ancho de banda de los filtros puede ser muy pequeño y selectivo, o muy amplio y no selectivo, dependiendo de los valores de R y C usados.
El centro o punto de frecuencia resonante es la media geométrica de los puntos de corte superior e inferior. En esta frecuencia central, la señal de salida está en su máximo y el desplazamiento de fase de la señal de salida es el mismo que el de la señal de entrada.
La amplitud de la señal de salida de un filtro de paso de banda o cualquier filtro RC pasivo para el caso, siempre será menor que la de la señal de entrada. En otras palabras, un filtro pasivo también es un atenuador que proporciona una ganancia de voltaje menor que 1 (Unidad). Para proporcionar una señal de salida con una ganancia de voltaje mayor que la unidad, se requiere alguna forma de amplificación dentro del diseño del circuito.
Un filtro de paso de banda pasiva se clasifica como un filtro de tipo de segundo orden porque tiene dos componentes reactivos dentro de su diseño, los condensadores. Se compone de dos circuitos de filtro RC individuales, cada uno de los cuales son filtros de primer orden.
Si se conectan más filtros en cascada, el circuito resultante se conocerá como un»filtro de orden n-ésimo», donde la «n» representa el número de componentes reactivos individuales y, por lo tanto, los polos dentro del circuito del filtro. Por ejemplo, los filtros pueden ser un 2nd-order,4ª-order,10ª-order, etc.
Cuanto mayores sean los filtros de orden más pronunciada será la pendiente en n veces -20dB / de cada. Sin embargo, un solo valor de condensador obtenido mediante la combinación de dos o más condensadores individuales sigue siendo un condensador.
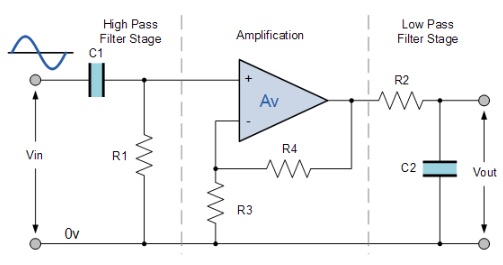
Nuestro ejemplo anterior muestra la curva de respuesta de frecuencia de salida para un filtro de paso de banda «ideal» con ganancia constante en la banda de paso y ganancia cero en las bandas de parada. En la práctica, la respuesta de frecuencia de este circuito de filtro de paso de banda no sería la misma que la reactancia de entrada del circuito de paso alto afectaría la respuesta de frecuencia del circuito de paso bajo (componentes conectados en serie o en paralelo) y viceversa. Una forma de superar esto sería proporcionar alguna forma de aislamiento eléctrico entre los dos circuitos de filtro, como se muestra a continuación:
Almacenamiento en búfer de etapas de filtro individuales

Una forma de combinar amplificación y filtrado en el mismo circuito sería utilizar un amplificador operacional o un amplificador operacional, y se dan ejemplos de estos en la sección Amplificador operacional. En el siguiente tutorial veremos los circuitos de filtro que utilizan un amplificador operacional dentro de su diseño no solo para introducir ganancia sino también para proporcionar aislamiento entre etapas. Estos tipos de arreglos de filtros se conocen generalmente como filtros activos.