Valor promedio del voltaje

El proceso de encontrar el voltaje promedio de una forma de onda alterna es muy similar a eso, la diferencia de encontrar el valor RMS esta vez es que los valores instantáneos no están al cuadrado y no podemos encontrar la raíz cuadrada de la media sumada.

El voltaje (o corriente) promedio de una forma de onda periódica, ya sea sinusoidal, cuadrada o triangular, se define como: «el cociente del área bajo la forma de onda con respecto al tiempo». En otras palabras, el promedio de todos los valores instantáneos a lo largo del eje del tiempo, siendo el tiempo un período completo (T).

Para una forma de onda periódica, el área sobre el eje horizontal es positiva mientras que el área debajo del eje horizontal es negativa. El resultado es que el valor medio de una cantidad alterna simétrica es, por tanto, cero (0), ya que el área sobre el eje horizontal (el semiciclo positivo) es la misma que el área debajo del eje (el semiciclo negativo) y, por lo tanto, se cancela, el uno al otro. Esto se debe a que al calcular los dos rangos, el rango negativo cancela el rango positivo y crea un voltaje promedio de cero.

Entonces, la media o media de una cantidad alterna simétrica, como una onda sinusoidal, es la media medida en solo la mitad de un ciclo porque, como acabamos de indicar, la media de un ciclo completo es independiente de la amplitud máxima cero.

Las condiciones eléctricas, la tensión y la media medida o incluso la corriente media se pueden utilizar tanto para formas de onda de CA como para cálculos de rectificación de CC. Los símbolos utilizados para representar un valor medio se redefinen: VAV o IAV.

Método gráfico del voltaje promedio 

Una vez más, considere solo la media onda positiva del tutorial anterior sobre voltaje RMS. El voltaje medio o promedio de una forma de onda se puede determinar nuevamente gráficamente con una precisión razonable utilizando valores instantáneos igualmente espaciados.

La mitad positiva de la forma de onda se divide en cualquier número de «n» partes iguales u ordenadas medias. La anchura de cada centro será, por tanto, será No grados (o t segundos) y la altura de cada centro será igual al valor instantáneo de la forma de onda en ese punto a lo largo del eje x de la forma de onda.

Método gráfico del voltaje promedio

Cada valor de ordenadas medias de la forma de onda de voltaje se suma al siguiente y la suma sumada de V1 a V12 se divide por el número de ordenadas medias utilizadas para obtener el «voltaje promedio«. Entonces, el voltaje promedio (VAV) es la suma media de las ordenadas centrales de la forma de onda de voltaje y se da como:

y para nuestro simple ejemplo anterior, el voltaje promedio se calcula como:

Entonces, como antes, nuevamente un voltaje alterno de 20 voltios pico varía durante medio ciclo de la siguiente manera:

Voltaje	6.2V	11.8V	16.2V	19.0V	20.0V	19.0V	16.2V	11.8V	6.2V	0V
ángulo	18o	36o	54o	72o	90o	108o	126o	144o	162o	180o

Por medio de tensión, el valor se calcula como:

Luego, el valor de voltaje promedio para medio ciclo se informa usando el método gráfico de la siguiente manera: 12.64 voltios.

Los métodos analíticos para el voltaje promedio

Cómo ya se mencionó, el voltaje promedio de una forma de onda periódica cuyas dos mitades son exactamente iguales, ya sea sinusoidal o no sinusoidal, durante un ciclo completo es cero. Luego, el valor promedio se obtiene sumando los valores instantáneos del voltaje en solo medio ciclo. En el caso de una onda no simétrica o compleja, el voltaje (o corriente) promedio debe medirse matemáticamente durante todo el ciclo periódico.

El promedio se puede encontrar matemáticamente aproximando el área bajo la curva en varios intervalos a la distancia o longitud de la base. Esto se puede hacer usando triángulos o rectángulos como se muestra.

Aproximación del área

Aproximando las áreas de los rectángulos debajo de la curva, podemos tener una idea aproximada del área real de cada uno. Al sumar todas estas áreas, se puede determinar el valor promedio. Si se usara un número infinito de rectángulos más pequeños y delgados, el resultado final sería más preciso a medida que se acercara a 2 / π.

El área bajo la curva se puede determinar mediante varios métodos de aproximación, como la regla trapezoidal de ordenadas, las centrales o la regla de Simpson. Entonces, el área matemática bajo el positivo de la onda periódica definida como V(t) semiciclo = Vp.cos (ωt) con un período de T usando integración se da como:

Donde: 0 y π son los límites de integración, ya que estamos determinando el valor promedio de la tensión durante medio ciclo. Entonces, la superficie finalmente se da cómo área bajo la curva = 2 VP. Ahora que conocemos el área bajo el semiciclo positivo (o negativo), podemos encontrar fácilmente el valor promedio del área positiva (o negativa) de una forma de onda sinusoidal integrando la magnitud sinusoidal durante medio ciclo y dividiendo por la mitad el período.

Por ejemplo, si el voltaje instantáneo de una sinusoide se da como: v = Vp.sinθ y el período de una sinusoide se da como: 2π, entonces:

Entonces, ¿qué se da como la ecuación estándar para el voltaje promedio de una onda sinusoidal ?, La ecuación es:

Ecuación del voltaje promedio

El voltaje promedio (VAV) de una forma de onda sinusoidal se determina multiplicando el pico por la constante valor de voltaje 0.637, que es dos dividido por pi (π). La tensión media, que también puede denominarse valor medio, depende del tamaño de la forma de onda y no depende de la frecuencia ni del ángulo de fase.

Por lo tanto, esta media (ya sea voltaje o corriente) de una forma de onda sinusoidal también se puede mostrar como un valor de CC equivalente de área y tiempo.

El valor promedio es cero durante un ciclo completo porque el área promedio positiva sería cancelada por el área promedio negativa (V, lo que da como resultado un voltaje promedio de cero durante un ciclo completo ciclo AVG – (-VAVG )) en la suma de las dos áreas desde una sinusoide.

En referencia a nuestro ejemplo gráfico anterior, el máximo (Vvoltajepk) se informó como 20 voltios. Utilizando el método analítico, la tensión media se calcula por tanto como:

VAV = Vpk x 0,637 = 20 x 0,637 = 12,74 voltios. 

Este es el mismo valor que para el método gráfico.

Para encontrar el valor pico de un valor de voltaje promedio dado, simplemente modifique la fórmula y divida por la constante. Por ejemplo, ¿cuál es el valor pico sinusoidal Vpk ,? si el valor promedio es 65 voltios

Vpk = VAV ≤ 0,637 = 65 ≤ 0,637 = 102 voltios

Tenga en cuenta que multiplicar el valor pico o máximo por la constante 0,637 se aplica ÚNICAMENTE a formas de onda sinusoidales.

Resumen del voltaje promedio

Cuando se trata de voltajes (o corrientes) de CA, el término valor promedio se utiliza generalmente durante un ciclo completo, mientras que el término valor medio se utiliza para la mitad del ciclo periódico.

El promedio de una forma de onda sinusoidal completa durante un ciclo completo es cero porque las dos mitades se cancelan entre sí, por lo que se toma el promedio de medio ciclo. El valor promedio de una onda sinusoidal de voltaje o corriente es 0.637 veces el valor pico (Vp o Ip. Esta relación matemática entre los promedios se aplica tanto a la corriente CA como a la tensión CA.

A veces es necesario poder calcular el valor de CC voltaje o corriente continua que son emitidos por un rectificador o un circuito de pulso como un circuito de motor PWM porque el voltaje o la corriente, aunque no se invierte, cambia continuamente. Dado que no hay inversiones de fase, el valor promedio y la raíz cuadrada media (raíz ) se utilizan -mean- cuadrado) este valor no es importante para este tipo de aplicación.

La principal diferencia entre un voltaje RMS y un voltaje promedio es que el valor medio de una onda periódica es el promedio de todas las áreas instantáneas tomadas bajo la curva durante un período de la forma de onda y, en el caso de una magnitud sinusoidal, este período es se considera que es la mitad del semiciclo positivo, se utiliza generalmente en aras de la simplicidad. El cuadrado (RMS) de la forma de onda es el poder valor calorífico efectivo de valores de la onda comparado con un valor de CC constante y es la raíz cuadrada de la media de los cuadrados de los instantáneos tomados durante un ciclo completo.

SOLO para una forma de onda sinusoidal pura, tanto el voltaje promedio como el voltaje RMS (o corrientes) se pueden calcular fácilmente como:

Promedio = 0.637 × valor máximo o pico, Vpk

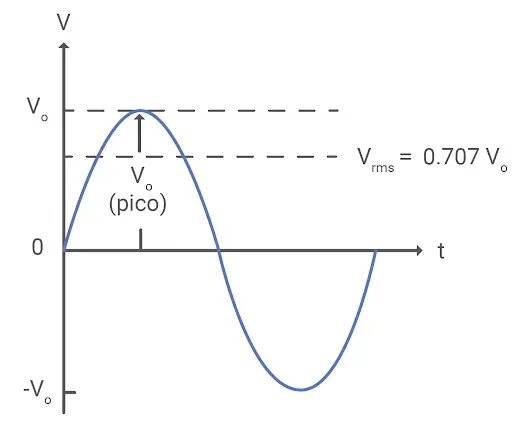
Valor RMS = 0.707 × valor máximo o pico, Vpk

Un comentario final sobre el uso de voltaje promedio y voltaje RMS. Ambos valores se pueden utilizar para representar el «factor de forma» de una forma de onda alterna sinusoidal. El factor de forma se define como la forma de una forma de onda de CA y es la raíz del voltaje cuadrático medio dividido por el voltaje medio (factor de forma = valor cuadrático medio de la raíz / valor medio).Para una forma de onda sinusoidal o compleja, el factor de forma se da como: (π / (2√2)), que es aproximadamente constante igual a 1,11. El factor de forma es una relación y, por lo tanto, no tiene unidades eléctricas. Si se conoce el factor de forma de una forma de onda sinusoidal, el voltaje promedio se puede determinar usando el valor de voltaje RMS, y viceversa, ya que el voltaje promedio es 0.9 veces el valor de voltaje RMS de una onda sinusoidal.