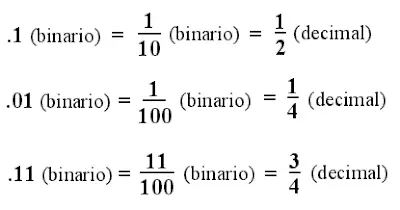Las fracciones binarias utilizan el mismo principio de ponderación que los números decimales, excepto que cada dígito binario utiliza el sistema de numeración de base 2.
Sabemos que los decimales o (números denarios) usan el sistema de numeración de base diez (base-10), donde cada dígito de un número decimal puede tomar uno de los diez valores posibles en el rango de 0 a 9. Así que al moverse de derecha a izquierda a lo largo de un número decimal, cada dígito tendrá un valor diez veces mayor que el dígito a su derecha inmediata.
Pero además de que cada dígito es diez veces más grande que el número anterior a medida que nos movemos de derecha a izquierda, cada dígito también puede ser diez veces más pequeño que su número vecino a medida que avanzamos en la dirección opuesta de izquierda a derecha.
Sin embargo, una vez que llegamos a cero (0) y al punto decimal, no necesitamos simplemente detenernos, sino que podemos continuar moviéndonos de izquierda a derecha a lo largo de los dígitos produciendo lo que generalmente se llama números fraccionarios.
Contenido
Un número fraccional típico

Aquí, en este ejemplo de número decimal (o denario), el dígito inmediatamente a la derecha del punto decimal (número 5) vale un décimo (1/10 o 0,1) del dígito inmediatamente a la izquierda del decimal punto (número 4) que como valor de multiplicación de uno (1).
Por lo tanto, a medida que avanzamos por el número de izquierda a derecha, cada dígito subsiguiente será una décima parte del valor del dígito inmediatamente a su posición izquierda, y así sucesivamente.
Luego, el sistema de numeración decimal utiliza el concepto de valores de ponderación posicionales o relativos produciendo una notación posicional, donde cada dígito representa un valor ponderado diferente dependiendo de la posición ocupada a cada lado del punto decimal.
Por lo tanto, matemáticamente en el sistema de numeración denario estándar, estos valores se escriben comúnmente como: 40, 31, 22, 13 para cada posición a la izquierda del punto decimal en nuestro ejemplo anterior. Asimismo, para los números fraccionarios a derecha del punto decimal, el peso del número se convierte en dar más negativo: 5-1,6-2,7-3, etc.
Así podemos ver que cada dígito en el sistema decimal estándar indica la magnitud o peso de ese dígito dentro del número. Entonces, el valor de cualquier número decimal será igual a la suma de sus dígitos multiplicada por sus respectivos pesos, por lo que para nuestro ejemplo anterior: N = 1234.56710 en el formato decimal ponderado, esto también será igual:
1000 + 200 + 30 + 4 + 0.5 + 0.06 + 0.007 = 1234.56710
o podría escribirse para reflejar la ponderación de cada dígito denario:
(1 × 1000) + (2 × 100) + (3 × 10) + (4 × 1) + (5 × 0.1) + (6 × 0.01) + (7 × 0.001) = 1234.56710
o incluso en forma polinomial como:
(1 × 103) + (2 × 102) + (3 × 101) + (4 × 100) + (5 × 10-1) + (6 × 10-2) + (7 ×10-3) = 1234.56710
También podemos usar esta idea de notación posicional donde cada dígito representa un valor ponderado diferente dependiendo de la posición que ocupa en el sistema de numeración binario. La diferencia esta vez es que el sistema numérico binario (o simplemente de números binarios) es un sistema posicional, donde las diferentes posiciones ponderadas de los dígitos son elevadas a la potencia de 2 (base 2) en lugar de 10.
Fracciones binarias
El sistema de numeración binario es un sistema de numeración de base 2 que contiene sólo dos dígitos, un «0» o un «1». Así, cada dígito de un número binario puede tomar el valor «0» o «1» con la posición del 0 o 1 indicando su valor o ponderación. Pero también podemos tener una ponderación binaria para valores menores que 1 produciendo lo que se llaman números binarios fraccionarios sin signo.
De manera similar a las fracciones decimales, los números binarios también se pueden representar como números fraccionarios sin signo colocando los dígitos binarios a la derecha del punto decimal o, en este caso, el punto binario. Por lo tanto, todos los dígitos fraccionarios a la derecha del punto binario tienen ponderaciones respectivas que son potencias negativas de dos, creando una fracción binaria. En otras palabras, las potencias de 2 son negativas.
Entonces, para los números binarios fraccionarios a la derecha del punto binario, el peso de cada dígito se vuelve más negativo dando: 2-1, 2-2,2-3,2-4, y así sucesivamente como se muestra.
Fracciones binarias

etc.
Por lo tanto, si tomamos la fracción binaria de 0.10112, entonces se toman en cuenta los pesos posicionales para cada uno de los dígitos dando su equivalente decimal de:

Para este ejemplo, la conversión de fracción decimal del número binario 0.10112 es 0.687510.
Ejemplo de fracciones binarias No.1
Ahora supongamos que tenemos el siguiente número binario de: 1101.01112, cuál será su número decimal equivalente.
1101.0111 = (1 × 23) + (1 × 22) + (0 × 21) + (1 × 20) + (0 × 2-1) + (1 × 2-2) + (1 × 2-3) + (1 ×2-4)
= 8 + 4 + 0 + 1 + 0 + 1/4 + 1/8 + 1/16
= 8 + 4 + 0 + 1 + 0 + 0.25 + 0.125 + 0.0625 =
Por lo tanto, el número decimal equivalente de 1101.01112 se da como: 13.437510
Entonces podemos ver que los números binarios fraccionarios, es decir, los números binarios que tienen una ponderación menor que 1 (20), se pueden convertir en su número decimal equivalente, dividiendo sucesivamente el factor de ponderación binario por el valor de dos para cada disminución de la potencia de 2, recordando también que 20 es igual a 1, y no a cero.
Otros ejemplos de fracciones binarias
0.11 = (1 × 2-1) + (1 × 2-2) = 0.5 + 0.25 = 0.7510
11.001 = (1 × 21) + (1 × 20) + (1 ×2-3) = 2 + 1 + 0,125 = 3.12510
1011,111 = (1 × 23) + (1 × 21) + (1 × 20) (1 × 2-1) + (1 × 2-2) + (1 ×2-3)
= 8 + 2 + 1 + 0.5 + 0.25 + 0.125 = 11.87510
Conversión de un decimal a una fracción binaria
La conversión de una fracción decimal a un número binario fraccionario se logra usando un método similar al que usamos para los números enteros. Sin embargo, esta vez se usa la multiplicación en lugar de la división con los números enteros en lugar de los restos, siendo el dígito de acarreo el equivalente binario de la parte fraccionaria del número decimal.
Al convertir de decimal a binario, la parte entera (secuencia positiva de derecha a izquierda) y la parte fraccionaria (secuencia negativa de izquierda a derecha) del número decimal se calculan por separado.
Para la parte entera del número, el equivalente binario se encuentra dividiendo sucesivamente (conocida como división sucesiva) la parte entera del número decimal repetidamente por 2 (÷ 2), anotando los restos en orden inverso desde el bit menos significativo (LSB ) al bit más significativo (MSB), hasta que el valor se convierta en «0» produciendo el equivalente binario.
Así que para encontrar el equivalente binario del número entero decimal: 11810
118 (divide por 2) = 59 plus resto 0 (LSB)
59 (divide por 2) = 29 plus resto 1 (↑)
29 (divide por 2) = 14 plus resto 1 (↑)
14 (dividir entre 2) = 7 más resto 0 (↑)
7 (dividir entre 2) = 3 más resto 1 (↑)
3 (dividir entre 2) = 1 más resto 1 (↑)
1 (dividir por 2) = 0 más resto 1 (MSB)
Entonces el equivalente binario de 11810 es, por lo tanto:
La parte fraccionaria del número se encuentra multiplicando sucesivamente (conocida como multiplicación sucesiva) la parte fraccionaria dada de la número decimal repetidamente por 2 (× 2), observando los acarreos en orden hacia adelante, hasta que el valor se convierte en «0» produciendo el equivalente binario.
Entonces, si el proceso de multiplicación produce un producto mayor que 1, el acarreo es un «1» y si el proceso de multiplicación produce un producto menor que «1», el acarreo es un «0».
Tenga en cuenta también que si los procesos de multiplicación sucesivos no parecen dirigirse hacia un cero final, el número fraccionario tendrá una longitud infinita o hasta que se haya obtenido el número equivalente de bits, por ejemplo, 8 bits o 16 bits, etc. dependiendo del grado de precisión requerido.
Entonces, para encontrar la fracción binaria equivalente a la fracción decimal: 0.812510
0.8125 (multiplicar por 2) = 1.625 = 0.625 carry 1 (MSB)
0.625 (multiplicar por 2) = 1.25 = 0.25 carry 1 (↓)
0.25 ( multiplicar por 2) = 0.50 = 0.5 acarreo 0 (↓)
0.5 (multiplicar por 2) = 1.00 = 0.0 acarreo 1 (LSB)
Por lo tanto, el equivalente binario de
Podemos verifique esta respuesta usando el procedimiento anterior para convertir una fracción binaria en un número decimal equivalente: 0.1101 = 0.5 + 0.25 + 0.0625 = 0.812510
Ejemplo de fracciones binarias No.2
Encuentre la fracción binaria equivalente al siguiente número decimal: 54.6875
Primero convertimos el entero 54 a un número binario de la forma normal utilizando la división sucesiva desde arriba.
54 (dividir entre 2) = 27 resto 0 (LSB)
27 (dividir entre 2) = 13 resto 1 (↑)
13 (dividir entre 2) = 6 resto 1 (↑)
6 (dividir entre 2) = 3 resto 0 ( ↑)
3 (dividir por 2) = 1 resto 1 (↑)
1 (dividir entre 2) = 0 resto 1 (MSB)
Por lo tanto, el equivalente binario de 5410 es: 1101102
A continuación, convertimos la fracción decimal 0.6875 en un binario fracción usando multiplicaciones sucesivas.
0.6875 (multiplicar por 2) = 1.375 = 0.375 acarreo 1 (MSB)
0.375 (multiplicar por 2) = 0.75 = 0.75 acarreo 0 (↓)
0.75 (multiplicar por 2) = 1.50 = 0.5 acarreo 1 (↓ )
0.5 (multiplicar por 2) = 1.00 = 0.0 acarreo 1 (LSB)
Por lo tanto, el equivalente binario de
Por lo tanto, el equivalente binario del número decimal: 54.687510 es 110110.10112
Resumen de fracciones binarias
Hemos visto aquí en este tutorial sobre Fracciones Binarias que para convertir cualquier fracción decimal en su fracción binaria equivalente, debemos multiplicar la parte fraccionaria decimal, y solo la parte fraccionaria decimal por 2 y registrar el dígito que aparece a la izquierda del punto binario. Este dígito binario que es el dígito de acarreo SIEMPRE será un «0» o un «1».
Luego debemos multiplicar la fracción decimal restante por 2 nuevamente repitiendo la secuencia anterior usando multiplicaciones sucesivas hasta que la fracción se reduzca a cero o se haya completado la cantidad requerida de bits binarios para una fracción binaria repetida. Los números fraccionarios están representados por potencias negativas de 2.
Para números decimales mixtos debemos realizar dos operaciones separadas. División sucesiva para la parte entera a la izquierda del punto decimal y multiplicación sucesiva para la parte fraccionaria a la derecha del punto decimal.
Tenga en cuenta que la parte entera de un número decimal mixto siempre tendrá un número binario exacto equivalente, pero la parte decimal fraccionaria puede que no, ya que podríamos obtener una fracción repetida que resulte en un número infinito de dígitos binarios si quisiéramos representar la fracción decimal exactamente.