Filtro de Sallen-Key

El diseño del filtro de Sallen-Key es una topología de filtro activo de segundo orden que podemos usar como bloques de construcción básicos para implementar circuitos de filtro de orden superior , como circuitos de filtro de paso bajo (LPF), paso alto (HPF) y paso de banda (BPF).

Como hemos visto en esta sección de filtros, los filtros electrónicos, pasivos o activos, se utilizan en circuitos en los que solo se requiere una amplitud de señales en un rango limitado de frecuencias. La ventaja de utilizar filtros Sallen-Key es que son fáciles de implementar y comprender.

La topología de Sallen y Key es un diseño de filtro activo basado en un solo amplificador operacional no inversor y dos resistencias, creando así un diseño de fuente de voltaje controlado por voltaje (VCVS) con características de filtro de alta impedancia de entrada, baja impedancia de salida y buena estabilidad y, como tal, permite que las secciones individuales de los filtros Sallen-key se unan en cascada para producir filtros de orden mucho más alto.

Pero antes de analizar el diseño y el funcionamiento del filtro Sallen-key, primero recordemos las características de un solo resistor-condensador o red RC cuando se somete a un rango de frecuencias de entrada.

El divisor de voltaje

Cuando dos (o más) resistencias se conectan juntas a través de un voltaje de suministro de CC, se desarrollarán diferentes valores de voltaje en cada resistor creando lo que básicamente se llama un divisor de voltaje o una red de divisores de potencial.

Divisor de voltaje resistivo

El circuito básico que se muestra consta de dos resistores en serie conectados a través de un voltaje de entrada, VIN.

La ley de Ohm nos dice que el voltaje que cae a través de una resistencia es la suma de la corriente que fluye a través de ella multiplicada por su valor resistivo, V = I * R, por lo que si las dos resistencias son iguales, entonces la tensión cae en ambas resistencias, R1 y R2 también será igual y se dividirá equitativamente entre ellos.

El voltaje desarrollado o caído a través del resistor R2 representa el voltaje de salida, VOUT y viene dado por la relación de los dos resistores y el voltaje de entrada. Por lo tanto, la función de transferencia para esta simple red de divisores de voltaje se da como:

Función de transferencia del divisor de voltaje resistivo

Pero, ¿qué pasaría con el voltaje de salida, VOUT si cambiamos el voltaje de entrada a una fuente o señal de CA y variamos su rango de frecuencia? Bueno, en realidad nada, ya que las resistencias generalmente no se ven afectadas por los cambios en la frecuencia (excluidas las bobinas de alambre), por lo que su respuesta de frecuencia es cero, lo que permite que los voltajes de CA, Irms caigan de 2* R a través de las resistencias de la misma manera que lo sería para una constante estado de los voltajes de CC.

El divisor de voltaje RC

Si cambiamos la resistencia R1 anterior a un capacitor, C como se muestra, ¿cómo afectaría eso a nuestra función de transferencia anterior? Sabemos por nuestros tutoriales sobre condensadores que un condensador se comporta como un circuito abierto una vez cargado cuando se conecta a una fuente de voltaje de CC.

Divisor de voltaje RC

Por lo tanto, cuando se conecta un suministro de CC de estado estable a VIN, el capacitor se cargará completamente después de 5 constantes de tiempo (5T = 5RC) y en ese tiempo no extrae corriente del suministro. Por lo tanto, no hay corriente fluyendo a través de la resistencia, R y no se desarrolló una caída de voltaje a través de ella, por lo que no hay voltaje de salida. En otras palabras, los condensadores bloquean los voltajes de CC de estado estable una vez cargados.

Si ahora cambiamos el suministro de entrada a un voltaje sinusoidal de CA, las características de este circuito RC simple cambian por completo a medida que se bloquea la CC o la parte constante de la señal. Entonces ahora estamos analizando el circuito RC en el dominio de la frecuencia, que es la parte de la señal que depende del tiempo.

En un circuito de CA, un capacitor tiene la propiedad de reactancia capacitiva, XC pero aún podemos analizar el circuito RC de la misma manera que lo hicimos con los circuitos de solo resistencias, la diferencia es que la impedancia del capacitor ahora depende de la frecuencia .

Para circuitos y señales de CA, la reactancia capacitiva (XC) es la oposición al flujo de corriente alterna a través de un capacitor medido en ohmios. La reactancia capacitiva depende de la frecuencia, es decir, a bajas frecuencias (ƒ ≅ 0) el capacitor se comporta como un circuito abierto y los bloquea.

A muy altas frecuencias (ƒ ≅ ∞) el capacitor se comporta como un cortocircuito y pasa las señales directamente a la salida como VOUT = VIN. Sin embargo, en algún lugar entre estos dos extremos de frecuencia el condensador tiene una impedancia dada por xC. Entonces, nuestra función de transferencia del divisor de voltaje desde arriba se convierte en:

Por lo tanto, los cambios en la frecuencia provocan cambios en XC, lo que provoca cambios en la magnitud del voltaje de salida. Considere el circuito a continuación:

Circuito de filtro RC

El gráfico muestra la respuesta de frecuencia de este simple circuito de primer orden RC. A bajas frecuencias, la ganancia de voltaje es extremadamente baja, ya que la señal de entrada está bloqueada por la reactancia del condensador. A altas frecuencias, la ganancia de voltaje es alta (unidad) ya que la reactancia hace que el capacitor se convierta efectivamente en un cortocircuito a estas altas frecuencias, por lo que VOUT = VIN

Sin embargo, se convierte en un punto de frecuencia donde la reactancia del capacitor es igual a la resistencia de la resistencia, es decir: XC = R y esto se llama punto de «frecuencia crítica», o más comúnmente llamado frecuencia de corte o frecuencia de esquina ƒC.

Como la frecuencia de corte ocurre cuando XC = R, la ecuación estándar utilizada para calcular este punto de frecuencia crítica se da como:

Ecuación de frecuencia de corte

La frecuencia de corte, ƒC define desde dónde cambia el circuito, en este ejemplo atenuando o bloqueando todas las frecuencias por debajo de ƒC y comienza a pasar todas las frecuencias por encima de este punto ƒC. Por lo tanto, el circuito se denomina «filtro de paso alto».

La frecuencia de corte es donde la relación de la señal de entrada a salida tiene una magnitud de 0,707 y cuando se convierte a decibelios es igual a –3dB. Esto a menudo se conoce como un punto de bajada de filtros de 3dB.

Como la reactancia del capacitor está relacionada con la frecuencia, es decir, la reactancia capacitiva (XC) varía inversamente con la frecuencia aplicada, podemos modificar la ecuación del divisor de voltaje anterior para obtener la función de transferencia de este simple circuito de filtro de paso alto RC como se muestra:

Circuito de filtro RC

Una de las principales desventajas de un filtro RC es que la amplitud de salida siempre será menor que la entrada, por lo que nunca puede ser mayor que la unidad. Además, la carga externa de la salida por más etapas o circuitos RC afectará las características de los filtros. Una forma de superar este problema es convertir el filtro RC pasivo en un “Filtro RC activo” agregando un amplificador operacional a la configuración RC básica.

Al agregar un amplificador operacional, el filtro RC básico se puede diseñar para proporcionar una cantidad requerida de ganancia de voltaje en su salida, cambiando así el filtro de un atenuador a un amplificador. Además, debido a la alta impedancia de entrada y la baja impedancia de salida de un amplificador operacional, evita la carga externa del filtro, lo que permite que se ajuste fácilmente en un amplio rango de frecuencia sin alterar la respuesta de frecuencia diseñada.

Considere el filtro simple de paso alto activo RC a continuación:

Filtro de paso alto activo

La parte del filtro RC del circuito responde de la misma manera que la anterior, es decir, pasa las frecuencias altas pero bloquea las frecuencias bajas, con la frecuencia de corte establecida por los valores de R y C. El amplificador operacional o amplificador operacional para abreviar, está configurado como un amplificador no inversor cuya ganancia de voltaje se establece por la relación de las dos resistencias, R1 y R2.

Luego, la ganancia de voltaje de lazo cerrado, AV en la banda de paso de un amplificador operacional no inversor se da como:

Ecuación de frecuencia de corte

Ejemplo de filtro simple de primer orden RC No.1

Un filtro requiere un paso alto activo para tener un corte fuera de frecuencia de 500Hz y una ganancia de banda de paso de 9dB. Calcule los componentes necesarios asumiendo que se utiliza un amplificador operacional estándar 741.

Desde arriba, hemos visto que la frecuencia de corte, ƒC está determinada por los valores de R y C en el circuito RC selectivo en frecuencia. Si asumimos un valor para R de 5kΩ (cualquier valor razonable sería suficiente), entonces el valor de C se calcula como:

El valor calculado de C es 63.65nF, por lo que el valor preferido más cercano utilizado es 62nF.

La ganancia del filtro de paso alto en la región de la banda de paso debe ser + 9dB, lo que equivale a una ganancia de voltaje, AV de 2.83. Suponga un valor arbitrario para la resistencia de retroalimentación, R1 de 15 kΩ, esto da un valor para la resistencia R1 de:

Nuevamente, el valor calculado de R2 es 8197Ω. El valor preferido más cercano sería 8200Ω o 8.2kΩ. Esto nos da el circuito final para nuestro ejemplo de filtro de paso alto activo de:

Circuito de filtro de paso alto

Hemos visto que se puede hacer un filtro de paso alto de primer orden simple usando una sola resistencia y condensador que produzca una frecuencia de punto de corte fc. Donde la amplitud de salida es –3dB por debajo de la amplitud de entrada. Al agregar una segunda etapa de filtro RC a la primera, podemos convertir el circuito en un filtro de paso alto de segundo orden.

Filtro de segundo orden RC

El filtro de segundo orden RC más simple consta de dos secciones RC en cascada juntas como se muestra. Sin embargo, para que esta configuración básica funcione correctamente, las impedancias de entrada y salida de las dos etapas RC no deben afectar el funcionamiento de la otra, es decir, no deben interactuar.

Circuito de filtro de paso alto 

La conexión en cascada de una etapa de filtro RC con otra (valores RC idénticos o diferentes) no funciona muy bien porque cada etapa sucesiva carga la anterior y cuando se agregan más etapas RC, el punto de frecuencia de corte se aleja más de la frecuencia deseada o requerida.

Una forma de superar este problema para un diseño de filtro pasivo es tener la impedancia de entrada de la segunda etapa RC al menos 10 veces mayor que la impedancia de salida de la primera etapa RC. Eso es en la frecuencia de corte RB = 10 * R1 y CB = CA/ 10.

La ventaja de aumentar los valores de los componentes en un factor de 10 es que el filtro de segundo orden resultante produce una caída más pronunciada de 40 dB / década que las etapas RC en cascada. Pero, ¿qué pasa si desea diseñar un filtro de orden 4º o 6º, entonces el cálculo de diez veces el valor de los componentes anteriores puede llevar mucho tiempo y ser complicado?

Una forma simple de conectar en cascada etapas de filtro RC que no interactúan ni se cargan entre sí para crear filtros de orden superior (las secciones de filtro individuales no necesitan ser idénticas) que se pueden sintonizar y diseñar fácilmente para proporcionar la ganancia de voltaje requerida es usar un filtrado de etapas Sallen-key.

Filtros Sallen y Key

Sallen-Key es una de las mayoría de las configuraciones de filtro común para el diseño de primer orden (1st-orden) y filtro de segundo orden (2nd-orden) y como tal se utiliza como los bloques de construcción básicos para la creación de muchos filtros de orden superior.

Las principales ventajas del diseño de filtro de Sallen-key son:

• Simplicidad y comprensión de su diseño básico.
• El uso de un amplificador no inversor para aumentar la ganancia de voltaje.
• Los diseños de filtro de primer y segundo orden se pueden conectar en cascada fácilmente de paso bajo y paso alto. 
• Las etapas se pueden conectar en cascada juntas.
• Cada etapa RC puede tener una ganancia de voltaje diferente.
• Replicación de componentes y amplificadores RC.
• Las etapas Sallen-key de segundo orden tienen una caída pronunciada de 40dB / década que la RC en cascada.

Sin embargo, existen algunas limitaciones para la clave Sallen básica diseño de filtro en el que la ganancia de voltaje, AV y el factor de aumento Q, están estrechamente relacionados debido al uso de un amplificador operacional dentro del diseño de clave de Sallen. Casi cualquier Q Se puede realizar de valor mayor que 0.5, ya que al usar una configuración no inversora, la ganancia de voltaje, AV siempre será mayor que 1, (unidad) pero debe ser menor que 3, de lo contrario se volverá inestable.

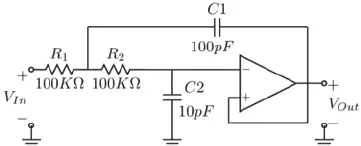
La forma más simple de diseño de filtro Sallen-key es usar valores iguales de condensadores y resistencias (pero las C y las R no tienen que ser iguales), con el amplificador operacional configurado como un búfer de ganancia unitaria como se muestra. Tenga en cuenta que la resistencia RA ya no está conectada a tierra, sino que proporciona retroalimentación positiva para el amplificador.

Circuito de filtro de paso alto Sallen-Key

Los componentes pasivos CA, RA, CB y RB forman el circuito selectivo de frecuencia de segundo orden. Por lo tanto, a bajas frecuencias, los condensadores CA y CB aparecen como circuitos abiertos, por lo que la entrada la señal está bloqueada y no hay salida. A frecuencias más altas, CA y CB aparecen en la señal de entrada sinusoidal como cortocircuitos, por lo que la señal se almacena directamente en la salida.

Sin embargo, alrededor del punto de frecuencia de corte, la impedancia de CA y CB será el mismo valor que RA y RB, como se indicó anteriormente, por lo que la retroalimentación positiva producida a través de CB proporciona una ganancia de voltaje Q y un aumento en la salida ampliación de la señal.

Dado que ahora tenemos dos conjuntos de redes RC, la ecuación anterior para la frecuencia de corte para un filtro Sallen-Key también se modifica:

Ecuación de frecuencia de corte Sallen-Key

Si los dos condensadores en serie CA y CB se igualan (Ca = CB =C) y las dos resistencias R y Rb también se hacen iguales (Ra = RB =R), entonces la anterior se simplifica ecuación para el original frecuencia de corte ecuación de:

A medida que la operativa, el amplificador está configurado como un búfer de ganancia unitaria, es decir, A = 1, la frecuencia de corte, ƒC y Q son completamente independientes entre sí, lo que permite un diseño de filtro más simple. Luego, el factor de aumento, Q se calcula como:

Por lo tanto, para la configuración del búfer de ganancia unitaria, la ganancia de voltaje (AV) del circuito del filtro es igual a 0.5, o -6dB (sobre amortiguado) en el punto de frecuencia de corte, y esperaríamos ver esto porque es una respuesta de filtro de segundo orden, como 0.7071 * 0.7071 = 0.5. Eso es -3dB * -3dB = -6dB.

Sin embargo, como el valor de Q determina las características de respuesta del filtro, la selección adecuada de los amplificadores operacionales dos resistencias de realimentación, R1 y R2, nos permite seleccionar la ganancia de banda de paso requerida A para el factor de ampliación elegido, Q.

Tenga en cuenta que para una topología de filtro de clave Sallen, seleccionar el valor de A para que esté muy cerca del valor máximo de 3, dará como resultado valores altos Q. Una Alta Q hará que el diseño del filtro sea sensible a las variaciones de tolerancia en los valores de las resistencias de retroalimentación R1 y R2. Por ejemplo, el establecimiento de la ganancia de tensión de 2,9 (A = 2,9) resultará en el valor de Q es 10 (1 / (3-2.9)), por lo que el filtro se convierte en alrededor extremadamente sensible ƒC.

Respuesta del filtro Sallen-key

Entonces podemos ver que cuanto menor sea el valor de Q, más estable será el diseño del filtro Sallen y Key. Si bien los valores altos de Q pueden hacer que el diseño sea inestable, con ganancias muy altas que produzcan un negativo Q se producirían oscilaciones.

Ejemplo de filtro de clave y Sallen No.2

Diseñe un paso alto de segundo orden filtro de clave y Sallen de circuito con las siguientes características: ƒC = 200Hzy Q = 3

Para simplificar un poco las matemáticas, asumiremos que los dos condensadores en serie CA y CB son iguales (CA = CB = C) y también las dos resistencias RA y RB son iguales (RA = RB = R).

El valor calculado de R es 7957Ω, por lo que el valor preferido más cercano utilizado es 8kΩ.

Para Q = 3, la ganancia se calcula como:

Si A = 2.667, entonces la relación de R1/ R2 = 1.667 como se muestra:

El valor calculado de R2 es 5998Ω, por lo que el valor preferido más cercano utilizó 6000Ω o 6kΩ. Esto luego nos da el circuito final para nuestro ejemplo de filtro de paso alto de:

Filtro de paso alto Sallen y Key

Luego, con una frecuencia de corte o esquina de 200Hz, una ganancia de banda de paso de 2.667 y una ganancia de voltaje máxima en el frecuencia de corte de 8 (2.667 * 3) debido a Q = 3, podemos mostrar las características de este filtro Sallen y Key de paso alto de segundo orden en el siguiente diagrama de Bode.

Gráfico del filtro de Bode, Sallen y Key

Resumen del filtro de Sallen-Key

Hemos visto aquí en este tutorial que la configuración Sallen-Key, también conocida como circuito de fuente de voltaje controlado por voltaje (VCVS) es la topología de filtro más utilizada debido principalmente a el hecho de que el amplificador operacional utilizado en su diseño puede configurarse como un búfer de ganancia unitaria o como un amplificador no inversor.

La configuración básica del filtro Sallen-key se puede utilizar para implementar diferentes respuestas de filtro, como Butterworth, Chebyshev o Bessel con la selección correcta de la red de filtros RC. La mayoría de los valores prácticos de R y C se pueden usar recordando que para un punto de frecuencia de corte específico, los valores de R y C son inversamente proporcionales. Es decir, a medida que el valor de R se hace más pequeño, C se vuelve más grande y viceversa.

La tecla Sallen es un filtro de diseño de segundo orden que puede ser en cascada, junto con otras etapas de RC para crear filtros de orden superior. No es necesario que varias etapas de filtro sean iguales, pero cada una puede tener una frecuencia de corte diferente o características de ganancia. Por ejemplo, armar una etapa de paso bajo y una etapa de paso alto para crear un filtro de paso de banda Sallen y Key.Aquí hemos analizado el diseño de un filtro de paso alto de clave Sallen, pero las mismas reglas se aplican igualmente para un diseño de paso bajo la ganancia de voltaje, AV del amplificador operacional, determina su respuesta y está establecida por las resistencias del divisor de voltaje. R1 y R2 recordando que la ganancia de voltaje debe ser menor que 3 , de lo contrario, el circuito del filtro se volverá inestable.