Diagramas fasoriales

Las formas de onda sinusoidales de la misma frecuencia pueden tener una diferencia de fase entre ellas que es la diferencia angular entre las dos formas de onda sinusoidales. Además, los términos «adelanto», «retraso», «en fase» y «fuera de fase» se utilizan comúnmente para indicar la relación de una forma de onda con otra con la expresión sinusoidal generalizada dada de la siguiente manera: A(t) = Am sen (ωt ± Φ) representa la forma sinusoidal en la forma del dominio del tiempo.

Sin embargo, cuando se representa matemáticamente de esta manera, a veces es difícil visualizar esta diferencia angular o de puntero entre dos o más formas de onda sinusoidales. Una forma de superar este problema son las curvas sinusoidales utilizando  diagramas fasor y esto se determina mediante el método del vector de rotación.

Básicamente, un vector giratorio, simplemente denominado «puntero«, es una línea escalada cuya longitud representa una cantidad de corriente alterna que tiene tanto la magnitud («amplitud máxima») como la dirección («fase») que «se congeló «en cualquier momento dado» se convierte en:

Un puntero es un vector con una punta de flecha en un extremo que parte del valor máximo del tamaño en el vector ( V o I ) y en parte el final del vector giratorio.

En general, se cree que los vectores en un extremo pivotan alrededor de un origen fijo conocido como «origen», mientras que el extremo de la flecha que representa la magnitud gira libremente sentido antihorario a una velocidad angular ( ω ) de una revolución completa para cada ciclo. Esta rotación en sentido antihorario del vector se considera una rotación positiva. Asimismo, una rotación en el sentido de las agujas del reloj se considera una rotación negativa.

Aunque los términos vectores y puntero se utilizan para describir una línea giratoria que es tanto de magnitud como de dirección en sí misma, la principal diferencia entre los dos es que una magnitud vectorial es el «pico» de la sinusoide, mientras que una magnitud de puntero es » El tamaño » del valor RMS «de la curva sinusoidal». En ambos casos, el ángulo de fase y la dirección siguen siendo los mismos.

La fase de una variable alterna en cualquier momento se puede representar mediante un diagrama vectorial, de modo que los diagramas vectoriales se pueden ver como «funciones del tiempo». Se puede construir una onda sinusoidal completa mediante un solo vector a una velocidad angular que gira ω = 2πƒ, donde ƒ es la frecuencia de la forma de onda. Entonces, un puntero es una cantidad que tiene tanto «tamaño» como «dirección».

En general, al crear un diagrama fasorial, siempre se asume que la velocidad angular de una onda sinusoidal es: ω en rad / s. Mira el diagrama fasorial a continuación:

Diagrama vectorial de una forma de onda sinusoidal

Si el vector único gira en sentido antihorario, su punta en el punto gira a completos 360°, o 2π, que es un ciclo completo. Si la longitud de su punta móvil se traza a lo largo del tiempo en un gráfico a diferentes intervalos angulares, como se muestra arriba, se dibujaría una forma de onda sinusoidal comenzando por la izquierda con el tiempo cero. Cada posición a lo largo del eje horizontal indica el tiempo que ha transcurrido desde el límite sin descompresión, t = 0. Si el vector es horizontal, el vértice del vector representa los ángulos en 0°, 180° y 360°.

Asimismo, si el pico del vector es vertical, pondrá el pico positivo, (+ Am) en 90° o π / 2, y el pico negativo, (-Am) en 270° o 3π /2, entonces el eje del tiempo de la forma de onda representará el ángulo en grados o radianes que movió el puntero. De modo que un puntero que representa un voltaje escalonado o un valor actual de un vector giratorio puede decir que está «congelado» en un cierto punto en el tiempo, (t) y en nuestro ejemplo anterior esto está en un ángulo de 30°.

A veces, cuando analizamos formas de onda alternas, necesitamos saber la posición del puntero que representa la cantidad alterna en un momento dado, especialmente cuando queremos comparar dos formas de onda diferentes en el mismo eje. Por ejemplo, voltaje y corriente. En la forma de onda anterior, asumimos que la forma de onda comienza en el tiempo t = 0 con un ángulo de fase correspondiente en grados o radianes.

Sin embargo, si una segunda forma de onda comienza a la izquierda o derecha de este punto cero, o si queremos representar la relación entre las dos formas de onda fasorial, debemos tener en cuenta esta diferencia de fase, Φ de la forma de onda. Considere el siguiente diagrama del anterior tutorial de fase de diferencia:

Diferencia de fase de una forma de onda sinusoidal

La expresión matemática generalizada para definir estas dos cantidades sinusoidales se escribe de la siguiente manera:

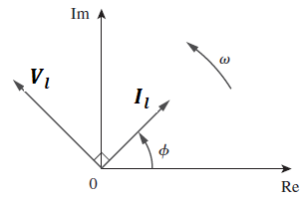
La corriente i está retrasada con respecto al voltaje, v en un ángulo Φ y en nuestro ejemplo anterior es 30°. La diferencia entre los dos fasores que representan las dos cantidades sinusoidales es el ángulo Φ, y el diagrama fasorial resultante es:

Diagrama vectorial de una forma de onda sinusoidal

El diagrama vectorial se dibuja según el tiempo cero ( t = 0 ) en el eje horizontal. Las longitudes de los fasores son proporcionales a los valores del voltaje (V) y la corriente (I) en el momento en el que se dibuja el diagrama fasorial. El puntero de corriente está ubicado en el ángulo detrás del puntero de voltaje Φ,ya que los dos giran en sentido antihorario como se indicó anteriormente, por lo que el ángulo Φ también se mide en la misma dirección en sentido antihorario.

Sin embargo, si las formas de onda estuvieran congeladas en el tiempo, t = 30s, el diagrama fasorial correspondiente se vería como el de la derecha. Nuevamente, el fasor de corriente va por detrás del fasor de voltaje porque las dos formas de onda tienen la misma frecuencia.

Sin embargo, dado que la forma de onda actual cruza la línea horizontal del eje cero en este momento, podemos usar el puntero actual como una nueva referencia y decir correctamente que el puntero de voltaje está «mostrando» el puntero actual por el ángulo Φ. En cualquier caso, un puntero se denomina puntero de referencia y todos los demás punteros van delante o detrás con respecto a esa referencia.

Adición de fasores

A veces, al estudiar ondas sinusoidales es necesario agregar dos formas de onda alternas, como en una conexión en serie de CA, que están desfasadas entre sí. Si están en fase, es decir, no hay desplazamiento de fase, se pueden sumar de la misma forma que los valores de CC para encontrar la suma algebraica de los dos vectores. Por ejemplo, si dos voltajes, como 50 voltios y 25 voltios, están «en fase» juntos, se suman o se suman a un voltaje de 75 voltios (50 + 25).

Sin embargo, si no están en fase, es decir, no tienen direcciones o puntos de partida idénticos, se debe tener en cuenta el ángulo de fase entre ellos para poder sumarlos juntos usando el diagramas fasor para determinar sus fasores resultantes o el vector suma usando la ley del paralelogramo.

Consideremos Voltajes de CA, tensión de V1 con un pico de 20 voltios y V2 con una tensión de pico de 30 voltios donde V1 líneas V2 alrededor de 60°. El total de voltaje VT de las dos tensiones se pueden determinar, primero dibuja un vector diagrama que muestra los dos vectores y luego se hace un paralelogramo en el que dos de los lados son voltajes V1 y V2, como se muestra a continuación:

Adición de puntero para dos punteros

Al dibujar los dos punteros para escalar en papel cuadriculado, su suma de punteros V1 + V2 se puede determinar fácilmente midiendo la longitud de la línea diagonal, que se llama el «vector r resultante», desde el punto cero hasta la intersección de las líneas de construcción 0-A. La desventaja de este método gráfico es que lleva tiempo dibujar los punteros a escala.

Si bien este método gráfico da una respuesta que es lo suficientemente precisa para la mayoría de los propósitos, puede crear un error si no se dibuja con precisión o a escala. Una forma de garantizar que siempre se obtenga la respuesta correcta es mediante una técnica analítica.

Matemáticamente, podemos sumar los dos voltajes determinando primero su dirección «vertical» y «horizontal», y a partir de esto, la componente «vertical» y «horizontal» para el «vector r» resultante  VT. Este método de análisis, que utiliza las reglas del coseno y del seno para encontrar este valor resultante, se denomina comúnmente forma rectangular.

En la forma rectangular, el puntero se divide en una parte real x y una parte imaginaria y, donde la forma la da la expresión generalizada  Z = x ± jy. (Discutiremos esto con más detalle en el próximo tutorial). Esto entonces nos da una expresión matemática que representa tanto la magnitud como la fase del voltaje sinusoidal como:

Definición de un sinusoidal complejo

Entonces la suma de dos vectores A y B usando la expresión generalizada anterior es la siguiente:

Adición de fasor usando la forma rectangular

El voltaje V2 de 30 voltios está en la dirección de referencia a lo largo del eje horizontal cero, entonces tiene un componente horizontal, pero no un componente vertical como sigue.

• • Componente horizontal = 30 cos 0° = 30 voltios
• • Componente vertical = 30 sin 0° = 0 voltiosEsto nos da la expresión rectangular para el voltaje V2 de:  30 + j0

El voltaje, V1 de 20 voltios lleva voltaje, V2 a 60°, entonces tiene componentes horizontales y verticales de la siguiente manera:

• • Componente horizontal = 20 cos 60° = 20 x 0.5 = 10 voltios
• • Componente vertical = 20 sin 60° = 20 x 0.866 = 17.32 voltios
• Esto entonces da la expresión rectangular para el voltaje V1 de:  10 + j17, 32

El resultado del voltaje VT se encuentra sumando los componentes horizontal y vertical de la siguiente manera:

• V Horizontal = suma de las reales de V1 y V2 = 30 + 10 = 40 voltios
• V Vertical = suma de las partes imaginarias de V1 y V2 = 0 + 17.32 = 17.32 voltios

Ahora que tanto el real como el encontrado también presentan el valor imaginario el tamaño de la tensión, VT está determinada simplificando el teorema de Pitágoras para un triángulo de 90° como se muestra:

Entonces el diagrama fasorial resultante será:

Valor resultante de VT

La resta fasorial

La resta fasorial es muy similar al método de suma rectangular anterior, excepto que esta vez la diferencia vectorial es la otra diagonal del paralelogramo entre los dos voltajes V1 y V2, como se muestra: 

La resta vectorial de dos punteros

Esta vez, en lugar de «sumar» los componentes horizontal y vertical, los quitamos, resta.

El diagrama vectorial trifásico

Hasta ahora sólo hemos considerado formas de onda de CA monofásicas en las que una sola bobina multivuelta gira dentro de un campo magnético. Pero si tres bobinas idénticas, cada una con el mismo número de vueltas de bobina, están dispuestas en un ángulo eléctrico de 120 en la fuente de alimentación en el mismo eje del rotor entre sí, se crearía una trifásica.

Una fuente de alimentación trifásica balanceada se compone de tres sinusoidales individuales de magnitud y frecuencia, pero están desfasados ​​entre sí en exactamente 120 grados eléctricos.

Por defecto, las tres fases están codificadas con colores rojo, amarillo y azul para identificar cada fase con la fase roja como fase de referencia. La secuencia de rotación normal para un suministro trifásico es rojo, seguido de amarillo, seguido de azul ( R, Y, B ).

Al igual que con los indicadores monofásicos anteriores, los indicadores que representan un sistema trifásico también giran en sentido antihorario alrededor de un punto central como lo indica la flecha etiquetada ω en rad / s. Los indicadores para un sistema trifásico simétrico de estrella o triángulo se muestran a continuación:

Diagrama vectorial trifásico

Los voltajes de fase son todos iguales, pero solo difieren en su ángulo de fase. Las tres alas de las bobinas están en los puntos a1, b1 y c1 conectados entre sí para producir una conexión neutra común para las tres fases individuales. Si se toma la fase roja como fase de referencia, cada voltaje de fase individual se puede definir en relación con el conductor neutro común.

Ecuaciones de voltaje trifásico

Si la tensión de la fase roja VRN S tomado como referencia del voltaje como lo mostrado anteriormente, la secuencia de fase es R – Y – B, de tensión de modo que la tensión en la fase amarilla VRN se retrasa 120° y la tensión en la fase azul se retrasa VYN por 120° también. Pero también podemos decir que la tensión de fase azul VBN dirige la fase roja VRN a 120°.

Un último punto en un sistema trifásico. Dado que los tres voltajes sinusoidales individuales tienen una relación fija de 120° entre sí, se denominan «equilibrados». Por lo tanto, en un conjunto de voltajes trifásicos balanceados, su suma vectorial es siempre cero como:  Va + Vb + V.c = 0

Resumen de los diagramas vectoriales 

En el sentido más simple, los diagramas vectoriales son una proyección de un vector giratorio sobre un eje horizontal que representa el valor instantáneo. Dado que se puede dibujar un diagrama vectorial para mostrar cualquier punto en el tiempo y, por lo tanto, cualquier ángulo, el puntero de referencia de una cantidad alterna siempre se dibuja a lo largo de la dirección positiva del eje x.

• Los vectores, fasores y diagramas de fasores SÓLO se aplican a cantidades de corriente alterna sinusoidal.
• Se puede utilizar un diagrama vectorial para representar dos o más cantidades sinusoidales estacionarias en cualquier momento.
• Generalmente, el puntero de referencia se dibuja a lo largo del eje horizontal, y es en este punto donde se dibujan los otros punteros. Todos los punteros se dibujan en relación con el eje cero horizontal.
• Se pueden dibujar diagramas vectoriales para mostrar más de dos ondas sinusoidales. Pueden ser voltaje, corriente o alguna otra cantidad alterna, pero la frecuencia de todos debe ser la misma.
• Todas las manecillas giran en sentido antihorario. Todos los punteros delante del puntero de referencia deben ser «iniciales», mientras que todos los punteros detrás del puntero de referencia deben estar «retrasados».
• En general, la longitud de un puntero representa el valor RMS de la cantidad sinusoidal en lugar de su valor máximo.
• Las curvas sinusales con diferentes frecuencias no se pueden mostrar en el mismo diagrama vectorial debido a la diferente velocidad de los vectores. En cualquier momento, el ángulo de fase entre ellos es diferente.
• Se pueden sumar o restar dos o más vectores y convertirse en un solo vector llamado Vector resultante.
• El lado horizontal de un vector corresponde al vector real o «x». El lado vertical de un vector es igual al vector imaginario o «y». La hipotenusa del triángulo rectángulo resultante corresponde al vector «r».
• En un sistema equilibrado trifásico, cada puntero individual está en 120°.

En el próximo tutorial de teoría de CA, veremos la representación de formas de onda sinusoidales como formas de números complejos en rectangulares  polares y exponenciales