Números complejos

Los números reales no son el único tipo de números que necesitamos usar, especialmente cuando se trata de fuentes y vectores sinusoidales dependientes de la frecuencia. Además de usar números normales o reales, se introdujeron números complejos para permitir resolver ecuaciones complejas usando números que son las raíces cuadradas de números negativos, √-1.

En ingeniería eléctrica, este tipo de número se denomina «número imaginario», y para distinguir un número imaginario de un número real, se utiliza la letra » j «, comúnmente en ingeniería eléctrica como el conocido operador j. Por tanto, la letra «j» se coloca delante de un número real para identificar su operación numérica imaginaria.

Ejemplos de números imaginarios son: j3, j12, j100 etc. Entonces un número complejo consta de dos partes diferentes pero muy relacionadas, un “número real” más un “número imaginario”.

Los números complejos representan puntos en un complejo bidimensional o plano S que están relacionados con dos ejes diferentes. El eje horizontal se denomina «eje real», mientras que el eje vertical se denomina «eje imaginario». La parte real y la parte imaginaria de un número complejo se abrevian como Re (z) e Im (z), respectivamente.

Los números complejos, que consisten en números reales (componente activo) e imaginarios (componente reactivo), se pueden sumar, restar y usar de la misma manera que el álgebra elemental para el análisis de circuitos CC.

Las reglas y leyes que se usan en matemáticas para sumar o restar números imaginarios son las mismas que para los números reales, j2 + j4 = j6, etc. La única diferencia está en la multiplicación, ya que dos números imaginarios que se multiplican juntos se convierten en un número negativo real . Los números reales también se pueden considerar como un número complejo, pero con una parte imaginaria de cero denotada por j0.

El operador j tiene un valor que es exactamente igual a √-1, por lo que la multiplicación sucesiva de » j » ( jxj ) da como resultado los siguientes valores de -1, -j  y +1. Dado que el operador j se usa a menudo para indicar la rotación en sentido antihorario de un vector, cada multiplicación sucesiva o fuerza de  «J», j2,j3, etc. forzará al vector a rotar un ángulo fijo de 90° en dirección contraria a las agujas del reloj, como se muestra a continuación. Si la multiplicación del vector da como resultado a -j-, el desplazamiento de fase operador también es -90°, es decir, una rotación en el sentido de las agujas del reloj.

Rotación vectorial del operador j

Al multiplicar un número imaginario con j2 el vector se  gira 180° en sentido antihorario, al multiplicar j3 por  270° y j4 se gira  360° de nuevo a su posición original. La multiplicación por j10 o j30 hace que el vector gire en sentido antihorario en la cantidad correspondiente. Con cada rotación sucesiva, el tamaño del vector siempre permanece igual.

En ingeniería eléctrica, hay varias formas de representar un número complejo de forma gráfica o matemática. Uno de esos métodos que utiliza la regla del coseno y del seno se llama forma cartesiana o rectangular.

Números complejos con forma rectangular

En el último tutorial sobre punteros, vimos que un número complejo está representado por una parte real y una parte imaginaria, que tienen la forma generalizada:

• Donde:
•   Z  – es el número complejo que representa el vector
•   x  – es la parte real o el componente activo
•   y  – es la parte imaginaria o el componente reactivo
•   j  – se define por √-1

En la forma rectangular, un número complejo se puede representar como un punto en un plano bidimensional llamado complejo o plano s. Por ejemplo, Z = 6 + j4 representa un solo punto cuyas coordenadas representan 6 en el eje real horizontal y 4 en el eje imaginario vertical, como se muestra:

Números complejos con el nivel complejo o S

Sin embargo, dado que tanto la parte real como la imaginaria de un número complejo en forma rectangular pueden ser un número positivo o negativo, tanto el eje real como el imaginario deben extenderse en direcciones tanto positivas como negativas. Esto luego crea un plano complejo con cuatro cuadrantes llamado diagrama de Argand como se muestra a continuación:

Diagrama de Argand de cuatro cuadrantes

En el diagrama de Argand, el eje horizontal representa todos los números reales positivos a la derecha del eje imaginario vertical y todos los números reales negativos a la izquierda del eje imaginario vertical. Todos los números imaginarios positivos se muestran sobre el eje horizontal, mientras que todos los números imaginarios negativos se muestran debajo del eje real horizontal. Esto luego crea un plano complejo bidimensional con cuatro cuadrantes diferentes etiquetados, QI, QII, QIII y QIV.

El diagrama de Argand anterior también se puede usar para representar un puntero giratorio, ya que un punto en el plano complejo, cuyo radio está dado por el tamaño del puntero, dibuja un círculo completo a tu alrededor durante 2π / ω segundos.

Luego, podemos expandir esta idea aún más para mostrar la definición de un número complejo en forma polar y rectangular para rotaciones de 90°.

Los números complejos también pueden tener partes reales o imaginarias de «cero»: Z = 6 + j0 o, por ejemplo, Z = 0 + j4. En este caso, los puntos se trazan directamente en el eje real o imaginario. Además, el ángulo de un número complejo puede calcularse usando trigonometría simple para calcular los ángulos de triángulos rectángulos, o medirse en sentido antihorario alrededor del diagrama de Argand comenzando desde el eje real positivo.

Entonces, los ángulos entre 0 y 90° están en el primer cuadrante ( I ), los ángulos ( θ ) entre 90° y 180° en el segundo cuadrante ( II ). El tercer cuadrante ( III ) contiene ángulos entre 180° y 270°, mientras que el cuarto y último cuadrante ( IV ), que cierra el círculo completo, contiene los ángulos entre 270° y 360° , etc. Los ángulos relevantes se pueden determinar en los cuatro cuadrantes de:

tan-1(componente imaginario ÷ componente real)

Suma y resta de números complejos

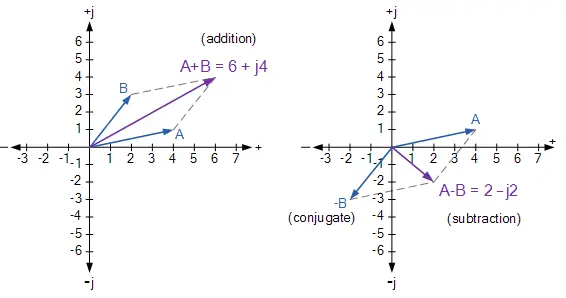
La suma o resta de números complejos se puede hacer matemática o gráficamente en forma rectangular. Además, las partes reales se agregan primero para formar la parte real de la suma y luego las partes imaginarias para formar la parte imaginaria de la suma, y ​​este proceso es el siguiente, usando dos números complejos A y B como ejemplos.

Sumas y restas de números complejos

Números complejos Ejemplo No. 1

Se definen dos vectores como A = 4 + j1 y B = 2 + j3, respectivamente . Determine la suma y la diferencia de los dos vectores tanto en forma rectangular ( a + jb ) como gráficamente como un diagrama de argumentos.

Suma y resta matemática

Suma

Resta

Sumas y restas gráficas

Multiplicación y división de números complejos

La multiplicación de números complejos en forma rectangular sigue más o menos las mismas reglas que para el álgebra normal, junto con algunas reglas adicionales para la multiplicación sucesiva del operador j, donde: j2 = – 1 Por ejemplo, nuestros dos vectores de arriba con A = 4 + j1 y si multiplica B = 2 + j3 juntos , obtiene el siguiente resultado:

Matemáticamente, la división de números complejos en forma rectangular es un poco más difícil de hacer porque la función conjugada de los denominadores debe usarse para convertir el denominador de la ecuación en un número real. Esto se conoce como «racionalización». Entonces, la división de números complejos se realiza mejor utilizando la «forma polar», que discutiremos más adelante. Sin embargo, como ejemplo en forma rectangular, podemos cambiar el valor del vector A dividido por el vector B determinado.

El complejo conjugado

El conjugado complejo o simplemente el conjugado de un número complejo, se encuentra simplemente invirtiendo el signo del número imaginario de los números complejos, manteniendo el signo del número real de la misma y sustituyendo el complejo conjugado de z el símbolo z . Por ejemplo, el conjugado z = 6 + j4 es z = 6 -j4, también el conjugado de z = 6 – J4 es z = 6 +j4.

Los puntos en el diagrama de Argand para un conjugado complejo tienen la misma posición horizontal en el eje real que el número complejo original, pero posiciones verticales opuestas. Por lo tanto, los conjugados complejos pueden verse como un reflejo de un número complejo. El siguiente ejemplo muestra un número complejo, 6 + j4 y su conjugado en el plano complejo.

Números complejos conjugados

La suma de un número complejo y su conjugado complejo siempre será un número real, como vimos anteriormente. Luego, la suma de un número complejo y su conjugado da el resultado sólo como un número real o componente activo, mientras que al restarlo solo se obtiene un número imaginario o componente reactivo. El conjugado de números complejos es un elemento importante utilizado en ingeniería eléctrica para determinar la potencia aparente de un circuito de CA utilizando una forma rectangular.

Números complejos con forma polar

A diferencia de la forma rectangular, que representa puntos en el plano complejo, la forma polar de un número complejo se escribe en términos de tamaño y ángulo. Por lo tanto, un vector de forma polar se representa como:  Z = A ∠ ± θ, donde: Z es el número complejo en forma polar, A es la magnitud o módulo del vector y θ es su ángulo o argumento de A , que puede sea ​​positivo o negativo. El tamaño y el ángulo del punto siguen siendo los mismos que para la forma rectangular anterior. Esta vez, la posición del punto en forma polar se representa en una «forma triangular» como se muestra a continuación.

Representación de forma polar de un número complejo

Dado que la representación polar de un punto se basa en la forma del triángulo, podemos usar la geometría simple del triángulo, y específicamente la trigonometría y el teorema de Pitágoras sobre triángulos, para encontrar tanto el tamaño como el ángulo del número complejo. Como recordamos de la escuela, la trigonometría se ocupa de la relación entre los lados y los ángulos de los triángulos, por lo que podemos describir las relaciones entre los lados de la siguiente manera:

Usando la trigonometría nuevamente, el ángulo θ de A se muestra de la siguiente manera:

Luego, en forma polar, representa la longitud de A y su ángulo el número complejo en lugar de un punto. Incluso en forma polar, el conjugado del número complejo tiene el mismo tamaño o módulo es el signo del ángulo que cambia, por ejemplo el conjugado de 6 ∠30°  6 ∠30° sería:

Conversión entre forma rectangular y forma polar

En la forma rectangular podemos expresar un vector en términos de sus coordenadas rectangulares, donde el eje horizontal es el eje real y el eje vertical es el eje imaginario o componente j. En forma polar, estos ejes reales e imaginarios están simplemente representados por “A ∠θ”. En nuestro ejemplo anterior, la relación entre la forma rectangular y la forma polar se puede definir como:

Conversión de la forma polar a una forma rectangular (P → R)

También podemos volver de la forma rectangular a la polar de la siguiente manera.

Conversión de la forma rectangular en una forma polar (R → P)

Multiplicación y división de la forma polar 

La forma rectangular es la mejor para sumar y restar números complejos como vimos anteriormente, pero la forma polar suele ser mejor para multiplicar y dividir Para dividir y multiplicar dos vectores en forma polar, primero debemos multiplicar los dos módulos o tamaños y luego sumar sus ángulos.

Multiplicación en forma polar

Multiplicar 6 ∠30° y 8 ∠- 45° en forma polar nos da.

División en forma polar

Para dividir dos vectores en forma polar necesitamos dividir los dos módulos y luego restar sus ángulos como se muestra:

Afortunadamente, las calculadoras científicas modernas de hoy en día han incorporado funciones matemáticas (consulte su libro) que permiten una conversión fácil de rectangular a polar ( R → P ) y viceversa de polar a rectangular ( R → P ).

Números complejos usando la exponencial

Hasta ahora hemos considerado los números complejos en la forma rectangular( a + jb ) y la forma polar( A ∠ ± θ ). Pero también hay un tercer método para representar un número complejo que es similar a la forma polar, que corresponde a la longitud (tamaño) y al ángulo de fase de la sinusoide, pero usa la base del logaritmo natural, e = 2.718 281 . Para encontrar el valor del número complejo. Este tercer método se llama forma exponencial.

La forma exponencial usa las funciones trigonométricas tanto del seno ( sin ) como del( coscos ) de un triángulo rectángulo para definir el exponencial complejo como el punto de pivote en el plano complejo. La forma exponencial para determinar la posición del punto se basa en la identidad de Euler, que lleva el nombre del matemático suizo Leonhard Euler, y es la siguiente:

La identidad de Euler se puede representar mediante el siguiente diagrama fasorial rotatorio en el plano complejo:

Podemos ver que la identidad de Euler es muy similar a la forma polar anterior, y que nos muestra que un número como Ae jθ, que tiene un tamaño de 1, también es un número complejo. No solo podemos convertir fácilmente números complejos que están en forma exponencial a formas polares como: 2e j30 convertirlo= 2∠30, 10e j120 = 10∠120 o -6e j90 = -6∠90, sino que también la identidad de Euler da una forma de convertir un número complejo de su forma exponencial a su forma rectangular. Luego, la relación entre formas exponenciales, polares y rectangulares al definir un número complejo se da de la siguiente manera:

Forma de números complejos

Notación de fasor

Hasta ahora hemos explorado varias formas de representar un vector giratorio o un vector estacionario, utilizando números complejos para definir un punto en el plano complejo. La notación de puntero es el proceso de construir un solo número complejo que tiene la amplitud y el ángulo de fase de la forma de onda sinusoidal dada.

Entonces la notación de puntero o la transformación de puntero, como a veces se le llama, transfiere la parte real de la función seno: A(t) = Am cos (ωt ± Φ) del dominio del tiempo al dominio de los números complejos, que también se llama dominio de la frecuencia, por ejemplo:

Ten en cuenta que √2 convierte la amplitud máxima en un eficaz valor RMS con el ángulo de fase especificado en radianes ω .

Resumen de números complejos

Para este tutorial sobre números complejos y el uso de números complejos en ingeniería eléctrica.

• Los números complejos constan de dos números diferentes, un número real más un número imaginario.
• Los números imaginarios se diferencian de los números reales mediante el uso del operador j.
• Un número con la letra » j » delante lo identifica como un número imaginario en el plano complejo.
• Por definición, el operador  j ≡ √-1
• Los números imaginarios se pueden sumar, restar, multiplicar y dividir como números reales.
• La multiplicación de » j » por » j » da como resultado j2 = -1.
• En forma rectangular, un número complejo está representado por un punto en el espacio en el plano complejo.
• En forma polar, un número complejo está representado por una línea, cuya longitud es la amplitud y el ángulo de fase.
• En forma exponencial, un número complejo se representa mediante una línea y el ángulo correspondiente que utilizan la base del logaritmo natural.
• Un número complejo se puede representar de tres formas:
  • Z = x + jy   »Forma rectangular
  • Z = A ∠Φ   » Forma polar
  • Z = A e jΦ   »Forma exponencial
• La identidad de Euler se puede utilizar para convertir números complejos de forma exponencial a rectangular.

En los tutoriales anteriores, incluido este, hemos visto que podemos usar punteros para representar formas de onda sinusoidales, y que su amplitud y ángulo de fase se pueden escribir en forma de un número complejo. También hemos visto que los números complejos se pueden representar en formas rectangulares, polares o exponenciales, y la conversión se produce entre cualquier forma de álgebra compleja, incluidas la suma, la resta, la multiplicación y la división.

En los próximos tutoriales sobre la relación fasorial en circuitos en serie de CA, examinaremos la impedancia de algunos componentes de circuitos pasivos comunes y dibujaremos los diagramas fasoriales tanto para la corriente que fluye a través del componente como para el voltaje que se le aplica comenzando con la resistencia alterna.