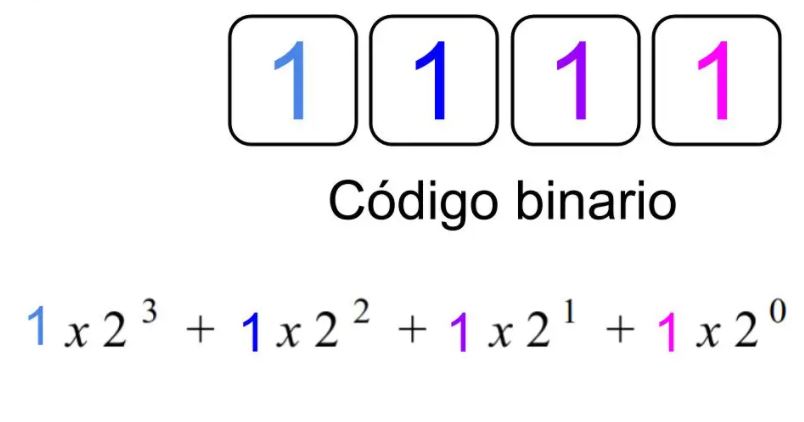
El decimal codificado en binario, o DCB, es otro proceso para convertir números decimales en sus equivalentes binarios. Como hemos visto en esta sección de tutoriales sobre números binarios, hay muchos códigos binarios diferentes que se utilizan en circuitos digitales y electrónicos, cada uno con su propio uso específico.
Como vivimos naturalmente en un mundo decimal (base 10), necesitamos alguna forma de convertir estos números decimales en un entorno binario (base 2) que las computadoras y los dispositivos electrónicos digitales entiendan, y el código decimal codificado en binario nos permite hacer eso.
Hemos visto anteriormente que un código binario de n bits es un grupo de «n» bits que asumen hasta 2n combinaciones distintas de unos y ceros. La ventaja del sistema decimal codificado en binario es que cada dígito decimal está representado por un grupo de 4 dígitos o bits binarios de la misma manera que el hexadecimal. Entonces, para los 10 dígitos decimales (0 a 9), necesitamos un código binario de 4 bits.
Pero no se confunda, el decimal codificado en binario no es lo mismo que el hexadecimal. Mientras que un número hexadecimal de 4 bits es válido hasta F16 que representa binario 11112, (15 decimal), los números decimales codificados tienen en el 9 binario 10012. Esto significa que aunque 16 números (24) se pueden representar usando cuatro dígitos binarios, en el sistema de numeración BCD las seis combinaciones de códigos binarios de: 1010 (decimal 10), 1011 (decimal 11), 1100 (decimal 12), 1101 ( decimal 13), 1110 (decimal 14) y 1111 (decimal 15) están clasificados como números prohibidos y no se pueden utilizar.
La principal ventaja del decimal codificado en binario es que permite una fácil conversión entre el formato decimal (base-10) y binario (base-2). Sin embargo, la desventaja es que el código BCD es un desperdicio ya que los estados entre 1010 (decimal 10) y 1111 (decimal 15) no se utilizan. Sin embargo, el decimal codificado en binario tiene muchas aplicaciones importantes, especialmente cuando se utilizan pantallas digitales.
En el sistema de numeración BCD, un número decimal se separa en cuatro bits por cada dígito decimal dentro del número. Cada dígito decimal está representado por su valor binario ponderado que realiza una traducción directa del número. Entonces, un grupo de 4 bits representa cada dígito decimal mostrado desde 0000 para un cero hasta 1001 para un nueve.
Entonces, por ejemplo, 35710 (Trescientos cincuenta y siete) en decimal se presentaría en decimal codificado en binario como:
35710 = 0011 0101 0111 (BCD)
Entonces podemos ver que BCD usa codificación ponderada, porque el bit binario de cada 4 el grupo de bits representa un peso dado del valor final. En otras palabras, el BCD es un código ponderado y los pesos usados en el código decimal codificado en binario son 8, 4, 2, 1, comúnmente llamado código 8421 ya que forma la representación binaria de 4 bits del dígito decimal relevante.
Contenido
Representación decimal codificada en binario de un número decimal
| Potencia binaria: | 23 | 22 | 21 | 20 |
| Peso binario: | 8 | 4 | 2 | 1 |
El peso decimal de cada dígito decimal a la izquierda aumenta en un factor de 10. En el sistema numérico BCD, el peso binario el peso de cada dígito aumenta en un factor de 2 como se muestra. Luego, el primer dígito tiene un peso de 1 ( 20 ), el segundo dígito tiene un peso de 2 ( 21 ), el tercero un peso de 4 ( 22 ), el cuarto un peso de 8 ( 23 ).
Luego, la relación entre los números decimales (denarios) y los dígitos decimales codificados en binarios ponderados se muestra a continuación.
Tabla de verdad para el decimal codificado en binario
| Número decimal | BCD 8421 Código | |
| 0 | 0000 0000 | |
| 1 | 0000 0001 | |
| 2 | 0000 0010 | |
| 3 | 0000 0011 | |
| 4 | 0000 0100 | |
| 5 | 0000 0101 | |
| 6 | 0000 0110 | |
| 7 | 0000 0111 | |
| 8 | 0000 1000 | |
| 9 | 0000 1001 | |
| 10 (1 + 0) | 0001 0000 | |
| 11 (1 + 1) | 0001 0001 | |
| 12 (1 + 2) | 0001 0010 | |
| … | … | |
| 20 (2 + 0) | 0010 0000 | |
| 21 (2 + 1) | 0010 0001 | |
| 22 (2 + 2) | 0010 0010 | |
| etc, continuando hacia arriba en grupos de cuatro |
Entonces podemos ver que el código BCD 8421 no es más que los pesos de cada dígito binario, con cada número decimal (denario) expresado como su equivalente binario puro de cuatro bits.
Conversión de decimal a BCD
Como hemos visto anteriormente, la conversión de decimal a decimal codificado en binario es muy similar a la conversión de hexadecimal a binario. En primer lugar, separe el número decimal en sus dígitos ponderados y luego escriba el código BCD 8421 de 4 bits equivalente que representa cada dígito decimal como se muestra.
Ejemplo de decimal codificado en binario No.1
Con la tabla anterior, convierta los siguientes números decimales (denarios): 8510, 57210 y 857910 en sus 8421 BCD equivalentes.
8510 = 1000 0101 (BCD)
57210 = 0101 0111 0010 (BCD)= 0101 0111 0010 (BCD)
857910 = 1000 0101 0111 1001 (BCD)
Tenga en cuenta que el número binario resultante después de la conversión será una verdadera traducción binaria de dígitos decimales. Esto se debe a que el código binario se traduce como un verdadero recuento binario.
Conversión de BCD a decimal
La conversión de decimal codificado en binario a decimal es exactamente lo contrario de lo anterior. Simplemente divida el número binario en grupos de cuatro dígitos, comenzando con el dígito menos significativo y luego escriba el dígito decimal representado por cada grupo de 4 bits. Agregue ceros adicionales al final si es necesario para producir una agrupación completa de 4 bits. Entonces, por ejemplo, 1101012 se convertiría en: 0011 01012 o 3510 en decimal.
Ejemplo de decimal codificado en binario No.2
Convierta los siguientes números binarios: 10012, 10102, 10001112 y 10100111000.1012 en sus equivalentes decimales.
10012 = 1001BCD = 910
10102 = esto producirá un error ya que es decimal 1010 y no es un número BCD válido.
10001112 = 0100 0111BCD = 4710
10100111000.1012 = 0101 0011 0001.1010BCD = 538.62510
La conversión de BCD a decimal o decimal a BCD es una tarea relativamente sencilla, pero debemos recordar que los números BCD son números decimales y no números binarios, aunque se representan mediante bits. Es importante comprender la representación BCD de un número decimal, porque los sistemas basados en microprocesadores utilizados por la mayoría de las personas deben estar en el sistema decimal.
Sin embargo, aunque BCD es fácil de codificar y decodificar, no es una forma eficaz de almacenar números. En la codificación estándar 8421 BCD de números decimales, el número de bits de datos individuales necesarios para representar un número decimal dado siempre será mayor que el número de bits necesarios para una codificación binaria equivalente.
Por ejemplo, en binario, un número decimal de tres dígitos de 0 a 999 requiere sólo 10 bits (11111001112), mientras que en decimal codificado en binario, el mismo número requiere un mínimo de 12 bits (0011 1110 0111BCD) para la misma representación.
Además, realizar tareas aritméticas con números decimales codificados en binario puede ser un poco incómodo ya que cada dígito no puede exceder de 9. La adición de dos dígitos decimales en BCD creará un posible bit de acarreo de 1 que debe agregarse al siguiente grupo de 4 bits.
Si la suma binaria con el bit de acarreo agregado es igual o menor que 9 (1001), el dígito BCD correspondiente es correcto. Pero cuando la suma binaria es mayor que 9, el resultado es un dígito BCD no válido. Por lo tanto, es mejor convertir los números BCD en binarios puros, realizar la suma requerida y luego convertir la parte posterior a BCD antes de mostrar los resultados.
No obstante, el uso de un sistema de codificación BCD tanto en microelectrónica como en sistemas informáticos es particularmente útil en situaciones en las que el decimal codificado en binario está destinado a mostrarse en una o más pantallas LED o LCD de 7 segmentos y hay muchos circuitos integrados populares disponibles que están configurados para dar una salida o salidas BCD.
Un IC común es el contador / divisor asíncrono 74LS90 que contiene contadores independientes de división por 2 y división por 5 que se pueden usar juntos para producir un contador de división por 10 décadas con salidas BCD. Otro es el 74LS390, que es una versión dual del 74LS90 básico, y también se puede configurar para producir una salida BCD.
Pero los IC codificados en BCD más utilizados son el 74LS47 y el 74LS48 BCD a decodificador / controlador de 7 segmentos, que convierte un código BCD de 4 bits de un contador, etc. y lo convierte en el código de visualización requerido para controlar los segmentos individuales de una pantalla LED de 7 segmentos. Si bien ambos IC son funcionalmente iguales, el 74LS47 tiene salidas activas bajas para controlar pantallas de ánodo común, mientras que el 74LS48 tiene salidas activas altas para controlar pantallas de cátodo común.
Decodificador decimal codificado en binario IC

Resumen de decimal codificado en binario
Hemos visto aquí que el decimal codificado en binario o BCD es simplemente la representación de código binario de 4 bits de un dígito decimal con cada dígito decimal reemplazado en las partes entera y fraccionaria con su equivalente binario. El código BCD usa cuatro bits para representar los 10 dígitos decimales del 0 al 9.
Entonces, por ejemplo, si quisiéramos mostrar números decimales en el rango de 0 a 9, (un dígito) necesitaríamos 4 bits de datos (un nibble ), números decimales en el rango de 0 a 99, (dos dígitos) necesitaríamos 8 bits (un byte), números decimales en el rango de 0 a 999, (tres dígitos) necesitaríamos 12 bits, y así. El uso de un solo byte (8 bits) para almacenar o mostrar dos dígitos BCD, lo que permite que un byte contenga un número BCD en el rango de 00 a 99, se conoce como BCD empaquetado.
El código decimal codificado en binario estándar se conoce comúnmente como un código BCD 8421 ponderado, con 8, 4, 2 y 1 que representan los pesos de los diferentes bits comenzando desde el bit más significativo (MSB) y avanzando hacia el bit menos significativo (LSB). Los pesos de las posiciones individuales de los bits de un código BCD son: 23 = 8, 22 = 4, 21 = 2, 20 = 1.La principal ventaja del sistema decimal codificado en binario es que es un sistema rápido y eficiente para convertir los números decimales en números binarios en comparación con el sistema binario puro. Pero el código BCD es un desperdicio ya que muchos de los estados de 4 bits (10 a 16) que no se utilizan, pero las pantallas decimales tienen aplicaciones importantes.