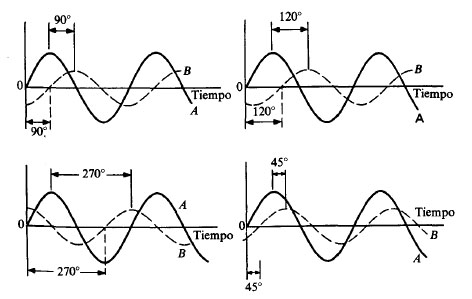
Diferencia de fase

Anteriormente vimos que una forma de onda sinusoidal es una cantidad alterna que se puede presentar gráficamente en el dominio del tiempo a lo largo de un eje horizontal cero. También vimos que, como una cantidad alterna, las ondas sinusoidales tienen un valor máximo positivo en el tiempo π / 2, un valor máximo negativo en el tiempo 3π / 2, con valores cero que ocurren a lo largo de la línea de base en 0, π y 2π.

Sin embargo, no todas las formas de onda sinusoidales pasarán exactamente a través del punto del eje cero al mismo tiempo, pero pueden “desplazarse” hacia la derecha o hacia la izquierda de 0o en algún valor en comparación con otra onda sinusoidal.

Por ejemplo, comparar una forma de onda de voltaje con la de una forma de onda de corriente. Esto luego produce un cambio angular o diferencia de fase entre las dos formas de onda sinusoidales. Cualquier onda sinusoidal que no pase por cero en t = 0 tiene un cambio de fase.

La diferencia de fase o cambio de fase, como también se le llama, de una forma de onda sinusoidal es el ángulo Φ (letra griega Phi), en grados o radianes, que la forma de onda se ha desplazado desde un cierto punto de referencia a lo largo del eje horizontal cero. En otras palabras, el cambio de fase es la diferencia lateral entre dos o más formas de onda a lo largo de un eje común y las formas de onda sinusoidales de la misma frecuencia pueden tener una diferencia de fase.

La diferencia de fase, Φ de una forma de onda alterna puede variar entre 0 y su período de tiempo máximo, T de la forma de onda durante un ciclo completo y esto puede estar en cualquier lugar a lo largo del eje horizontal entre, Φ = 0 a 2π (radianes) o Φ = 0 a 360o dependiendo de las unidades angulares utilizadas.

La diferencia de fase también se puede expresar como un desplazamiento de tiempo en T segundos que representa una fracción del período de tiempo, Y por ejemplo, + 10mS o – 50uS, pero generalmente es más común expresar la diferencia de fase como una medida angular.

Entonces, la ecuación para el valor instantáneo de una forma de onda de corriente o voltaje sinusoidal que desarrollamos en la forma de onda sinusoidal anterior deberá modificarse para tener en cuenta el ángulo de fase de la forma de onda y esta nueva expresión general se convierte en:

Ecuación de fase de diferencia

• Donde:
•   Am  – es la amplitud de la forma de onda.
•   ωt  – es la frecuencia angular de la forma de onda en radianes / seg.
•   Φ (phi): es el ángulo de fase en grados o radianes que la forma de onda se ha desplazado hacia la izquierda o hacia la derecha desde el punto de referencia.

Si la pendiente positiva de la forma de onda sinusoidal pasa por el eje horizontal «antes» de t = 0, entonces la forma de onda se ha desplazado hacia la izquierda de modo que Φ> 0, y el ángulo de fase será de naturaleza positiva, + Φ dando un ángulo de fase adelantado. En otras palabras, aparece antes de las 0° produciendo una rotación del vector en sentido antihorario.

Del mismo modo, si la pendiente positiva de la forma de onda sinusoidal pasa a través del eje x horizontal en algún momento «después» de t = 0, entonces la forma de onda se ha desplazado hacia la derecha, por lo que Φ <0, y el ángulo de fase será negativo en la naturaleza, lo que produce un ángulo de fase rezagado que aparece más tarde en el tiempo de 0° que produce una rotación del vector en el sentido de las agujas del reloj. Ambos casos se muestran a continuación:

Relación de fase de una forma de onda sinusoidal

En primer lugar, vamos a considerar que las dos cantidades alternas tales como voltaje, V y una corriente, tienen la misma frecuencia ƒ en Hertz. Como la frecuencia de las dos cantidades es la misma, la velocidad angular, ω también debe ser la misma. Entonces, en cualquier instante en el tiempo podemos decir que la fase de voltaje, v será la misma que la fase de la corriente i.

Entonces, el ángulo de rotación dentro de un período de tiempo particular será siempre el mismo y la diferencia de fase entre las dos cantidades de v e i será por lo tanto cero y Φ = 0. Como la frecuencia del voltaje, v y la corriente i son iguales, ambos deben alcanzar sus valores máximos positivos, negativos y cero durante un ciclo completo al mismo tiempo (aunque sus amplitudes pueden ser diferentes). Entonces las dos cantidades alternas, v e i, se dice que están «en fase».

Dos formas de onda sinusoidales: «en fase»

Ahora vamos a considerar que el voltaje, V y la corriente i tienen una diferencia de fase entre sí de  30º,por lo que (Φ  = 30o o π / 6 radianes). Como ambas cantidades alternas giran a la misma velocidad, es decir, tienen la misma frecuencia, esta diferencia de fase permanecerá constante para todos los instantes en el tiempo, entonces la diferencia de fase de 30° entre las dos cantidades está representada por phi Φ, como se muestra a continuación:

Diferencia de fase de una forma de onda sinusoidal

La forma de onda de voltaje anterior comienza en cero a lo largo del eje de referencia horizontal, pero en ese mismo instante de tiempo la forma de onda de la corriente sigue siendo de valor negativo y no cruza este eje de referencia hasta 30° más tarde. Entonces existe una diferencia de fase entre las dos formas de onda cuando la corriente cruza el eje de referencia horizontal alcanzando su pico máximo y valores cero después de la forma de onda de voltaje.

Como las dos formas de onda ya no están «en fase», deben estar «fuera de fase» en una cantidad determinada por phi Φ y, en nuestro ejemplo, esto es 30°. Entonces podemos decir que las dos formas de onda están ahora 30° desfasadas. También se puede decir que la forma de onda de la corriente está «retrasada» con respecto a la forma de onda de voltaje por el ángulo de fase, Φ. Luego, en nuestro ejemplo anterior, las dos formas de onda tienen una diferencia de fase rezagada, por lo que la expresión para el voltaje y la corriente anteriores se dará como:

  Donde, i se retrasa v en un ángulo Φ

Del mismo modo, si la corriente i tiene un valor positivo y cruza el eje de referencia alcanzando su pico máximo y valores cero en algún momento antes del voltaje v, entonces la forma de onda de la corriente estará «adelantada» el voltaje por algún ángulo de fase. Entonces se dice que las dos formas de onda tienen una diferencia de fase líder y la expresión tanto para el voltaje como para la corriente será:

  Donde, i adelanta v por ángulo Φ

El ángulo de fase de una onda sinusoidal se puede usar para describir la relación de una onda sinusoidal con otra usando los términos «Adelante» y «Retraso» para indicar la relación entre dos formas de onda sinusoidales de la misma frecuencia, trazada en el mismo eje de referencia. En nuestro ejemplo anterior, las dos formas de onda están desfasadas en 30°. Entonces, podemos decir correctamente que i se retrasa o podemos decir que v adelanta a i en 30°, dependiendo de cuál elijamos como referencia.

La relación entre las dos formas de onda y el ángulo de fase resultante se puede medir en cualquier lugar a lo largo del eje horizontal cero a través del cual pasa cada forma de onda con la dirección de la “misma pendiente”, ya sea positiva o negativa.

En los circuitos de alimentación de CA, esta capacidad para describir la relación entre un voltaje y una onda sinusoidal de corriente dentro del mismo circuito es muy importante y constituye la base del análisis de circuitos de CA.

La forma de onda del coseno

Ahora sabemos que si una forma de onda se “desplaza” hacia la derecha o la izquierda de 0° cuando se compara con otra onda sinusoidal, la expresión de esta forma de onda se convierte en Am sen (ωt ± Φ). Pero si la forma de onda cruza el eje horizontal cero con una pendiente positiva de 90° o π / 2 radianes antes de la forma de onda de referencia, la forma de onda se llama forma de onda de coseno y la expresión se convierte en:

Expresión de coseno

La onda del coseno, simplemente llamada «cos», es tan importante como la onda sinusoidal en la ingeniería eléctrica. La onda de coseno tiene la misma forma que su contraparte de onda sinusoidal, es decir, es una función sinusoidal, pero se desplaza en +90° o un cuarto de período completo por delante de ella.

Diferencia de fase entre una onda sinusoidal y una onda coseno

Alternativamente, también podemos decir que una onda sinusoidal es una onda de coseno que se ha desplazado en la otra dirección en -90°. De cualquier manera, cuando se trate de ondas sinusoidales u ondas cosenoidales con un ángulo, siempre se aplicarán las siguientes reglas.

Relaciones de onda seno y coseno

Al comparar dos formas de onda sinusoidales, es más común expresar su relación como seno o coseno con amplitudes positivas y esto se logra utilizando las siguientes identidades matemáticas:

Al usar estas relaciones anteriores, podemos convertir cualquier forma de onda sinusoidal con o sin una diferencia angular o de fase de una onda sinusoidal en una onda cosenoidal o viceversa.En el próximo tutorial sobre fasores usaremos un método gráfico para representar o comparar la diferencia de fase entre dos sinusoidales observando la representación fasorial de una cantidad de CA monofásica junto con algún álgebra fasorial relacionada con la suma matemática de dos o más fasores.